练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．化简：$\frac{{{x^2}-x}}{x+1}÷（{x-1-\frac{2x-2}{x+1}}）$．

    分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．

    解答 解：原式=$\frac{x（x-1）}{x+1}$÷$\frac{（x+1）（x-1）-2x+2}{x+1}$
    =$\frac{x（x-1）}{x+1}$•$\frac{x+1}{（x-1）^{2}}$
    =$\frac{x}{x-1}$．

    点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．已知一个数的两个平方根分别是2a-3和4-a，求这个数负的平方根是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．x2-y2=40，x+y=5，则x-y=8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

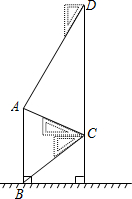    15．如图，中医药大学想把原来的校园内出现裂痕的李时珍的雕塑重新建造，为了和原来的高度一致，雕塑师小李为了测量其高度在教学楼二楼找到一点C，利用三角板测的雕塑顶端A点的仰角为30°，底部B点的俯角为45°，又在五楼找到一点D，利用三角板测得A点的俯角为60°．若CD为10米，求雕塑AB的高度（结果保留一位小数，$\sqrt{3}≈1.73$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．先化简，再求值：（$\frac{{a}^{2}-4}{{a}^{2}-4a+4}$-$\frac{2}{2-a}$）÷$\frac{2}{{a}^{2}-2a}$，其中a是方程x2+3x-10=0的根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

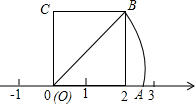    12．如图，正方形OABC的边长为2，OA在数轴上，以原点为圆心，对角线OB的长为半径画弧，交正半轴于一点D，则点D表示的实数是（　　）
    A．2.5B．2$\sqrt{2}$C．$\sqrt{5}$D．$\sqrt{7}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．大家知道，因式分解是数学中的一种重要的恒等变形，运用因式分解的思想方法有时能取得意想不到的效果，如化简：$\frac{1}{\sqrt{2}+1}$=$\frac{2-1}{\sqrt{2}+1}$=$\frac{（\sqrt{2}）^{2}-1}{\sqrt{2}+1}$=$\frac{（\sqrt{2}+1）（\sqrt{2}-1）}{\sqrt{2}+1}$=$\sqrt{2}$-1；
    $\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{3-2}{\sqrt{3}+\sqrt{2}}$=$\frac{（\sqrt{3}）^{2}-（\sqrt{2}）^{2}}{\sqrt{3}+\sqrt{2}}$=$\frac{（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}$-$\sqrt{2}$．
    （1）化简：$\frac{1}{\sqrt{4}+\sqrt{3}}$；
    （2）从以上化简结构中找出规律，写出用n（n≥1，且n为你整数）表示上面规律的式子；
    （3）根据以上规律计算：
    （$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+$\frac{1}{\sqrt{5}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2015}+\sqrt{2014}}$）（$\sqrt{2015}$+$\sqrt{2}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．化简：$\sqrt{8{x}^{3}{y}^{2}}$=2xy$\sqrt{2x}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．改革开放以来，我国国内生产总值由1978年的3645亿元增长到2014年的约63.6万亿元．将近似数63.6万亿元用科学记数法表示应为（　　）
    A．6.36×1012B．63.6×1012C．6.36×1013D．6.36×1014

    查看答案和解析>>

    同步练习册答案