
分析 (1)根据平方差公式,可分母有理化;
(2)根据观察,可发现规律:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$ (n≥1,且n为整数);
(3)根据规律,可得平方差公式,根据平方差公式,可得答案.
解答 解:(1)原式=$\frac{(\sqrt{4})^{2}-(\sqrt{3})^{2}}{\sqrt{4}+\sqrt{3}}$=$\frac{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}{\sqrt{4}+\sqrt{3}}$=$\sqrt{4}$-$\sqrt{3}$;
(2)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$ (n≥1,且n为整数);
(3)原式=($\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2015}$-$\sqrt{2014}$)($\sqrt{2015}$+$\sqrt{2}$)=($\sqrt{2015}$+$\sqrt{2}$)($\sqrt{2015}$-$\sqrt{2}$)=2015-2=2013.
点评 本题考查了分母有理化,利用平方差公式是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
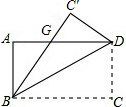 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.则△BDG的面积的值是( )| A. | 18.75cm2 | B. | 19.15cm2 | C. | 20cm2 | D. | 21.35cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 是原来的3倍 | B. | 不变 | C. | 是原来的$\frac{1}{3}$ | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com