
【题目】如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.
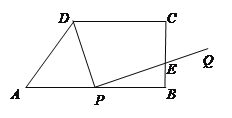
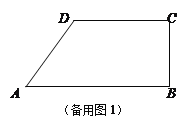

⑴当x为何值时,△APD是等腰三角形?
⑵若设BE=y,求y关于x的函数关系式;
⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
【答案】.
【解析】
⑴解:过D点作DH⊥AB于H,
则四边形DHBC为矩形,
∴DH=BC=4,HB=CD=6 ∴AH=2,AD=2![]() …………………1分
…………………1分
∵AP=x, ∴PH=x-2,
情况①:当AP=AD时,即x=2![]() ……………………………2分
……………………………2分
情况②:当AD=PD时,则AH=PH
∴2=x-2,解得x= 4………………………………………………………·3分
情况③:当AP=PD时,
则Rt△DPH中,x2=42+(x-2)2,解得x=5…………………………………4分
∵2<x<8,∴当x为2![]() 、4、5时,△APD是等腰三角形…………………………5分
、4、5时,△APD是等腰三角形…………………………5分
⑵易证:△DPH∽△PEB ………………………………………………………………7分
∴![]() ,∴
,∴![]() 整理得:y=
整理得:y=![]() (x-2)(8-x)=-
(x-2)(8-x)=-![]() x2+
x2+![]() x-4………8分
x-4………8分
⑶若存在,则此时BE=BC=4,即y=-![]() x2+
x2+![]() x-4=4,整理得:x2-10x+32=0
x-4=4,整理得:x2-10x+32=0
∵△=(-10)2-4×32<0,∴原方程无解,……………………………………………9分
∴不存在点P,使得PQ经过点C……………………………………………………10分
当BC满足0<BC≤3时,存在点P,使得PQ经过点C……………………………12分
1、过D点作DH⊥AB于H,则四边形DHBC为矩形,在Rt△AHD中,由勾股定理可求得DH、AD、PH的值,若△ADP为等腰三角形,则分三种情况:①当AP=AD时,x=AP=AD,②当AD=PD时,有AH=PH,故x=AH+PH,③当AP=PD时,则在Rt△DPH中,由勾股定理可求得DP的值,有x=AP=DP.
2、易证:△DPH∽△PEB![]() ,即
,即![]() ,故可求得y与x的关系式.
,故可求得y与x的关系式.
3、利用△DPH∽△PEB,得出![]() ,进而利用根的判别式和一元二次不等式解集得出即可.
,进而利用根的判别式和一元二次不等式解集得出即可.


科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习苏科版九下《锐角三角函数》一章时,小明同学对一个角的倍角的三角函数值是否具有关系产生了浓厚的兴趣,进行了一些研究.
(1)初步尝试:我们知道:tan60°= ,tan30°= ,发现结论:tanA 2tan![]() ∠A(填“=”或“≠”);
∠A(填“=”或“≠”);
(2)实践探究:如图1,在Rt△ABC中,∠C=90°,AC=2,BC=1,求tan![]() ∠A的值;小明想构造包含
∠A的值;小明想构造包含![]() ∠A的直角三角形:延长CA至D,使得DA=AB,连接BD,所以得到∠D=
∠A的直角三角形:延长CA至D,使得DA=AB,连接BD,所以得到∠D=![]() ∠A,即转化为求∠D的正切值.
∠A,即转化为求∠D的正切值.
请按小明的思路进行余下的求解:
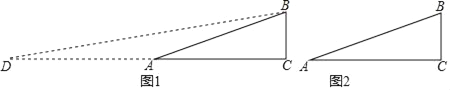
(3)拓展延伸:如图2,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .
.
①tan2A= ;
②求tan3A的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是【 】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣(2a+1)x+c(a>0)的图象经过坐标原点O,一次函数y=﹣x+4与x轴、y轴分别交于点A、B.
(1)c= ,点A的坐标为 ;
(2)若二次函数y=ax2﹣(2a+1)x+c的图象经过点A,求a的值;
(3)若二次函数y=ax2﹣(2a+1)x+c的图象与△AOB只有一个公共点,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数
在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数![]() 的图象于点M,△AOM的面积为3.
的图象于点M,△AOM的面积为3.

(1)求反比例函数的解析式;
(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数![]() 的图象上,求t的值.
的图象上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD,DE交BC于F,交AB的延长线于E,且∠EDB=∠C.
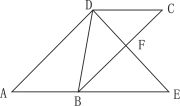
(1)求证:△ADE∽△DBE;
(2)若DE=9cm,AE=12cm,求DC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com