
分析 由已知条件腰长是30,底边长为x,根据三角形三边关系列出不等式,通过解不等式即可得到答案;设等腰三角形的腰长为a,则其底边长为:30-2a,根据三角形三边关系列不等式,求解即可.
解答 解:设底长为x,根据三边关系可知:30-30<x<30+30,
即0<x<60.
∴底长的取值范围是0<x<60.
设等腰三角形的腰长为a,则其底边长为:x,则x=30-2a.
∵30-2a-a<a<30-2a+a,
∴7.5<a<15,
∴腰长的取值范围是7.5<a<15,
底长的取值范围是0<x<7.5,
故答案为:0<x<60;7.5<a<15,0<x<7.5.
点评 本题考查等腰三角形的性质和三角形的三边关系的运用.列出不等式,通过解不等式求解是正确解答本题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD的边AB=4,BC=8,点P从A出发,以每秒2个单位沿A-B-C-D运动,同时点Q也从A出发,以每秒1个单位沿A-D运动,△APQ的面积为y,运动的时间为x秒,则y关于x的函数图象为( )
如图,矩形ABCD的边AB=4,BC=8,点P从A出发,以每秒2个单位沿A-B-C-D运动,同时点Q也从A出发,以每秒1个单位沿A-D运动,△APQ的面积为y,运动的时间为x秒,则y关于x的函数图象为( )| A. |  | B. | 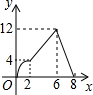 | C. | 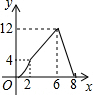 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com