
 已知:二次函数y=x2-(a+3)x+a+2(a为常数).
已知:二次函数y=x2-(a+3)x+a+2(a为常数).分析 (1)根据题意得抛物线与x轴只有一个公共点,利用抛物线与x轴的交点问题得到△=(a+3)2-4(a+2)=0,然后解方程即可得到a的值;
(2)①根据根与系数的关系得x1+x2=a+3,x1•x2=a+2,把x12+x22-x1x2=7变形得到(x1+x2)2-3x1•x2=7,则(a+3)2-3(a+2)=7,解得a1=-4,a2=1,然后利用c>0得到a=1,于是抛物线解析式为y=x2-4x+3;
②先求出A(1,0),B(3,0),C(0,3),则抛物线的对称轴为直线x=2,抛物线的顶点坐标为(2,-1),如图,再利用勾股定理计算出AC=$\sqrt{10}$,然后讨论:当AP=AC时,易得P1(2,3);当CP=CA时,以C点为圆心,$\sqrt{10}$为半径画弧交直线x=2于P2和P3,利用勾股定理计算出P1P2=P1P3=$\sqrt{6}$,于是可得到P2(2,3+$\sqrt{6}$),P3(2,3-$\sqrt{6}$).
解答 解:(1)∵抛物线与y一定有一个交点,
而抛物线与坐标轴只有两个交点,
∴抛物线与x轴只有一个公共点,
∴△=(a+3)2-4(a+2)=0,
整理得a2+2a+1=0,解得a1=a2=-1,
即a的值为-1;
(2)①根据根与系数的关系得x1+x2=a+3,x1•x2=a+2,
而x12+x22-x1x2=7,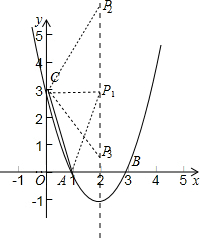
∴(x1+x2)2-3x1•x2=7,
∴(a+3)2-3(a+2)=7,
整理得a2+3a-4=0,解得a1=-4,a2=1,
而c>0,即a+2>0,
∴a=1,
∴抛物线解析式为y=x2-4x+3;
②存在.
当y=0时,x2-4x+3=0,解得x1=1,x2=3,则A(1,0),B(3,0),
当x=0时,y=x2-4x+3=3,则C(0,3),
∴抛物线的对称轴为直线x=2,抛物线的顶点坐标为(2,-1),如图,
AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
当AP=AC时,P1(2,3);
当CP=CA时,CP2=$\sqrt{10}$,而CP1=2,则P2P1=$\sqrt{(\sqrt{10})^{2}-{2}^{2}}$=$\sqrt{6}$,则P2(2,3+$\sqrt{6}$),同样方法得到P1P3=$\sqrt{6}$,所以P3(2,3-$\sqrt{6}$),
∴满足条件的P点坐标为(2,3)或(2,3+$\sqrt{6}$)或(2,3-$\sqrt{6}$).
点评 本题考查了二次函数综合题:熟练掌握二次函数的性质和等腰三角形的性质;理解抛物线与x轴的交点问题;会运用根与系数的关系求未知系数的值;会运用勾股定理计算线段的长.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
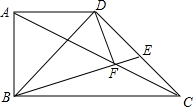 如图,直角梯形ABCD中,AD∥BC,AD=AB,AB⊥BC,BC=2AD,E为CD的中点,BE、AC交于点F,连接DF.下列结论:①△BCD为等腰直角三角形;②△ABC∽△EDB;③DF⊥BE;④AF=$\sqrt{2}$CF.其中正确的结论个数是( )
如图,直角梯形ABCD中,AD∥BC,AD=AB,AB⊥BC,BC=2AD,E为CD的中点,BE、AC交于点F,连接DF.下列结论:①△BCD为等腰直角三角形;②△ABC∽△EDB;③DF⊥BE;④AF=$\sqrt{2}$CF.其中正确的结论个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有五个村庄A、B、C、D、E,相互之间的路程如图所示(单位:km),现在要让五个村庄都通上网络,无论从哪里接入都可以,试问应怎样拉线才能使总费用最少?最少为多少?(每千米的费用为a元)
有五个村庄A、B、C、D、E,相互之间的路程如图所示(单位:km),现在要让五个村庄都通上网络,无论从哪里接入都可以,试问应怎样拉线才能使总费用最少?最少为多少?(每千米的费用为a元)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com