
����Ŀ��������һ�����⣺̽������![]() ��ͼ�������ʣ�С������ѧϰ�����ľ��飬�Ժ���
��ͼ�������ʣ�С������ѧϰ�����ľ��飬�Ժ���![]() ��ͼ�������ʽ�����̽����������С����̽�����̣��벹����ɣ�
��ͼ�������ʽ�����̽����������С����̽�����̣��벹����ɣ�
��1������![]() ���Ա���x��ȡֵ��Χ���� ����
���Ա���x��ȡֵ��Χ���� ����
��2���г�y��x�ļ����Ӧֵ����ֱ��д��m��ֵ��m=�� ����
��3������ƽ��ֱ������ϵxOy�У�������и��Զ�ӦֵΪ����ĵ㣬�������ú�����ͼ��
��4����Ϻ�����ͼ��д������![]() ��һ�����ʣ�
��һ�����ʣ�

���𰸡���1��x�٩�1����2��3����3������������4����x����1��x����1�Ͼ�����������
��������
��1�����ݷ�ĸ���㼴�ɵó�x+1��0����֮���ɵó��Ա���x��ȡֵ��Χ��
��2����y=![]() ���뺯������ʽ�����xֵ������
���뺯������ʽ�����xֵ������
��3����㡢����������ͼ����
��4���۲캯��ͼ����д��������һ�����ʼ�����
��1����x+1��0����x����1��
�ʴ�Ϊ��x����1��
��2����y=![]() =
=![]() ʱ�������x=3��
ʱ�������x=3��
�ʴ�Ϊ��3��
��3����㡢������ͼ����ͼ��ʾ��
��4���۲캯��ͼ��������������![]() ��x����1��x����1�Ͼ�����������
��x����1��x����1�Ͼ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ�˲�����¥��AC�ĸ߶ȣ��Ӿ���¥��C��![]() �ĵ�D����D��¥��C��ͬһˮƽ���ϣ���������б���¶�Ϊi=1��
�ĵ�D����D��¥��C��ͬһˮƽ���ϣ���������б���¶�Ϊi=1��![]() ��б��DBǰ��30�����B���ڵ�B�����¥��A������Ϊ53�㣬��¥��AC�ĸ߶ȣ��ο����ݣ�sin53���0.8��cos53���0.6��tan53���
��б��DBǰ��30�����B���ڵ�B�����¥��A������Ϊ53�㣬��¥��AC�ĸ߶ȣ��ο����ݣ�sin53���0.8��cos53���0.6��tan53���![]() ���������ø��ű�ʾ����ȡ����ֵ����
���������ø��ű�ʾ����ȡ����ֵ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10����ij��˾��Ӫһ���̲裬ÿǧ�˳ɱ�Ϊ50Ԫ���г����鷢�֣���һ��ʱ���ڣ�������w��ǧ���������۵���x��Ԫ/ǧ�����ı仯���仯�������ϵʽΪ��w����2x��240.�������̲������ʱ�����������Ϊy��Ԫ��������������⣺
��1����y��x�Ĺ�ϵʽ
��2����xȡ��ֵʱ���������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ȡij��һ�꣨��365��ƣ��е�30�����ƽ������״��ͳ�����£��¶ȣ�![]() ��
��
�¶ȣ� | 10 | 14 | 18 | 22 | 26 | 30 | 32 |
���� | 3 | 5 | 5 | 7 | 6 | 2 | 2 |
������������ݻش��������⣺
��1�����Ƹó�����ƽ�����´�Լ�Ƕ��٣�
��2���ϱ��е��¶����ݵ���λ����_______������_________��
��3������ó���һ����Լ�м������ƽ������Ϊ![]() ?
?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ɶ������ض��������֤����������������в�ͬ�����е��������������С������У�����ϲ�ķ��֣�������ȫ�ȵ�ֱ����������ͼ1��ͼ2�ڷ�ʱ���������������������֤����������С������ͼ1֤�����ɶ����Ĺ��̣�
������ȫ�ȵ�ֱ�������ΰ�ͼ1��ʾ�ڷţ�������DAB=90������֤��a2+b2=c2.
֤��������DB������D��BC���ϵĸ�DF����DF=EC=b��a��
��S�ı���ADCB=S��ACD+S��ABC= 12 b2+ 12 ab��
����S�ı���ADCB=S��ADB+S��DCB= 12 c2+ 12 a��b��a��
�� 12 b2+ 12 ab= 12 c2+ 12 a��b��a��
��a2+b2=c2
���������֤��������ͼ2��������֤����
������ȫ�ȵ�ֱ�������ΰ�ͼ2��ʾ�ڷţ�������DAB=90������֤��a2+b2=c2 ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ:��ƽ��ֱ������ϵ��,��֪![]() ���������������ֱ�Ϊ
���������������ֱ�Ϊ![]() ,
,![]() ,
,![]() .
.

��1����![]() ����ƽ��
����ƽ��![]() ����λ����,������ƽ��
����λ����,������ƽ��![]() ����λ����,�õ�
����λ����,�õ�![]() ,�뻭��
,�뻭��![]() ����
����![]() ,
,![]() ,
,![]() �Ķ�Ӧ��ֱ�Ϊ
�Ķ�Ӧ��ֱ�Ϊ![]() ,
,![]() ,
,![]() ��
��
��2���뻭����![]() ����
����![]() ��ԳƵ�
��ԳƵ�![]() ����
����![]() ,
,![]() ,
,![]() �Ķ�Ӧ��ֱ�Ϊ
�Ķ�Ӧ��ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
��3�����![]() ,
,![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �ֱ�����
�ֱ�����![]() ��
��![]() Ϊб�ߵ�ֱ�������Σ�
Ϊб�ߵ�ֱ�������Σ�![]() ��
��![]() �ǵȱ�������.
�ǵȱ�������.
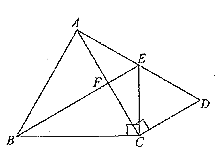
��1����֤��![]() ��
��
��2����![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪����������![]() ��һ�κ���
��һ�κ���![]() ��ͼ���ڵ�A.
��ͼ���ڵ�A.
��1�����A�����ꣻ
��2����x����һ��P��a��b��������P��x��Ĵ��ߣ�����λ�ڵ�A���Ҳࣩ���ֱ�![]() ��
��![]() ��ͼ���ڵ�B��C������OC����BC=
��ͼ���ڵ�B��C������OC����BC=![]() OA������OBC�����.
OA������OBC�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У�ֱ��![]() ��y�ύ�ڵ�
��y�ύ�ڵ�![]() ������ͼ��ʽ��������
������ͼ��ʽ��������![]() ��
��![]() ��
��![]() ��������
��������![]() ��
��![]() ��
��![]() ������ֱ��
������ֱ��![]() �ϣ���
�ϣ���![]() ��
��![]() ��
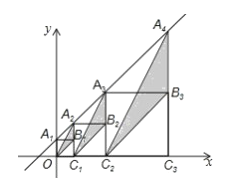
��![]() ��������x���ϣ�ͼ����Ӱ���������ε�������������μ�Ϊ
��������x���ϣ�ͼ����Ӱ���������ε�������������μ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() _______��
_______��![]() ________.���ú�n�Ĵ���ʽ��ʾ��nΪ��������
________.���ú�n�Ĵ���ʽ��ʾ��nΪ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com