
ЁОЬтФПЁПЮЊСЫНтБОаЃОХФъМЖбЇЩњЦкФЉЪ§бЇПМЪдЧщПіЃЌаЁССдкОХФъМЖЫцЛњГщШЁСЫвЛВПЗжбЇЩњЕФЦкФЉЪ§бЇГЩМЈЮЊбљБОЃЌЗжЮЊAЃЈ100ЁЋ90ЗжЃЉЁЂBЃЈ89ЁЋ80ЗжЃЉЁЂCЃЈ79ЁЋ60ЗжЃЉЁЂDЃЈ59ЁЋ0ЗжЃЉЫФИіЕШМЖНјааЭГМЦЃЌВЂНЋЭГМЦНсЙћЛцжЦГЩШчЯТЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМНтД№вдЯТЮЪЬтЃК
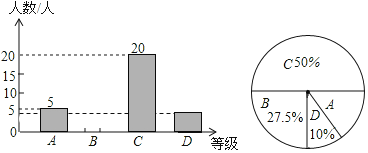
ЃЈ1ЃЉетДЮЫцЛњГщШЁЕФбЇЩњЙВгаЁЁ ЁЁШЫЃЛ
ЃЈ2ЃЉетИібЇаЃОХФъМЖЙВгабЇЩњ1200ШЫЃЌШєЗжЪ§ЮЊ80ЗжЃЈКЌ80ЗжЃЉвдЩЯЮЊгХауЃЌЧыЙРМЦетДЮОХФъМЖбЇЩњЦкФЉЪ§бЇПМЪдГЩМЈЮЊгХауЕФбЇЩњШЫЪ§ДѓдМгаЁЁ ЁЁШЫЃЛ
ЃЈ3ЃЉDЕШМЖЕФЫФЮЛбЇЩње§КУЪЧСНЮЛФаЩњКЭСНЮЛХЎЩњЃЌаЁССЯыЫцЛњВЩЗУЦфжаЕФСНЮЛЃЌЧыгУЪїзДЭМЛђСаБэЗЈМЦЫуаЁССВЩЗУЕФбЇЩњЧЁКУЪЧвЛФавЛХЎЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ40ЃЛЃЈ2ЃЉ480ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнCЕШМЖШЫЪ§МАЦфЫљеМАйЗжБШПЩЕУзмШЫЪ§ЃЛ
ЃЈ2ЃЉЯШгУБЛЕїВщЕФзмШЫЪ§ГЫвдBЕШМЖЖдгІАйЗжБШЧѓГіЦфШЫЪ§ЃЌдйгУзмШЫЪ§ГЫвдбљБОжаAЁЂBЕШМЖШЫЪ§КЭЫљеМБШР§МДПЩЕУЃЛ
ЃЈ3ЃЉЛЪїзДЭМЕУГіЫљгаЕШПЩФмЕФЧщПіЪ§ЃЌевГівЛФавЛХЎЕФЧщПіЪ§ЃЌМДПЩЧѓГіЫљЧѓЕФИХТЪЃЎ
НтЃКЃЈ1ЃЉетДЮЫцЛњГщШЁЕФбЇЩњЙВга20ЁТ50%ЃН40ЃЈШЫЃЉЃЌ
ЙЪД№АИЮЊЃК40ЃЛ
ЃЈ2ЃЉBЕШМЖШЫЪ§ЮЊ40ЁС27.5%ЃН11ЃЈШЫЃЉЃЌ
ЁрЙРМЦетДЮОХФъМЖбЇЩњЦкФЉЪ§бЇПМЪдГЩМЈЮЊгХауЕФбЇЩњШЫЪ§ДѓдМга1200ЁС![]() ЃН480ЃЈШЫЃЉЃЌ
ЃН480ЃЈШЫЃЉЃЌ
ЙЪД№АИЮЊЃК480ЃЛ
ЃЈ3ЃЉЛЪїзДЭМШчЯТЃК
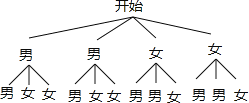
ЫљгаЕШПЩФмЕФЧщПіга12жжЃЌЦфжавЛФавЛХЎга8жжЃЌ
ЫљвдаЁССВЩЗУЕФбЇЩњЧЁКУЪЧвЛФавЛХЎЕФИХТЪЮЊ![]() ЃН
ЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
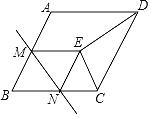
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌЁЯBЃН60ЁуЃЌABЃН2ЃЌMЮЊБпABЕФжаЕуЃЌNЮЊБпBCЩЯвЛЖЏЕуЃЈВЛгыЕуBжиКЯЃЉЃЌНЋЁїBMNбижБЯпMNелЕўЃЌЪЙЕуBТфдкЕуEДІЃЌСЌНгDEЁЂCEЃЌЕБЁїCDEЮЊЕШбќШ§НЧаЮЪБЃЌBNЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
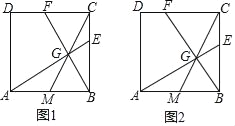
ЁОЬтФПЁПвбжЊе§ЗНаЮABCDЃЌЕуMЮЊБпABЕФжаЕуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕуGЮЊЯпЖЮCMЩЯЕФвЛЕуЃЌЧвЁЯAGB=90ЁуЃЌбгГЄAGЁЂBGЗжБ№гыБпBCЁЂCDНЛгкЕуEЁЂFЃЎ
ЂйЧѓжЄЃКBE=CFЃЛ
ЂкЧѓжЄЃКBE2=BCCEЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌдкБпBCЩЯШЁвЛЕуEЃЌТњзуBE2=BCCEЃЌСЌНгAEНЛCMгкЕуGЃЌСЌНгBGВЂбгГЄНЛCDгкЕуFЃЌЧѓtanЁЯCBFЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтбЇЩњМйЦкЕФПЮЭтдФЖСЧщПіЃЌФГаЃЫцЛњГщВщСЫАЫФъМЖбЇЩњдФЖСПЮЭтЪщЕФВсЪ§ВЂзїСЫЭГМЦЃЌЛцжЦГіШчЯТЭГМЦЭМЃЌЦфжаЬѕаЮЭГМЦЭМвђЮЊЦЦЫ№ЖЊЪЇСЫдФЖС5ВсЪщЕФЪ§ОнЃЌИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
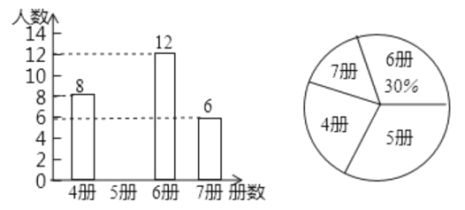
ЃЈ1ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМжаЖЊЪЇЕФЪ§ОнКЭЩШаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉдФЖСПЮЭтЪщВсЪ§ЕФжкЪ§ЮЊ______ВсЃЛ
ЃЈ3ЃЉИљОнЫцЛњГщВщЕФетИіНсЙћЃЌЧыЙРМЦИУаЃ1200УћбЇЩњжаПЮЭтЪщдФЖС7ВсЪщЕФбЇЩњШЫЪ§ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
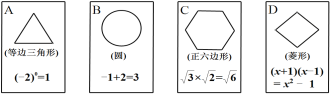
ЁОЬтФПЁПЖдШЮвтвЛИіЫФЮЛЪ§![]() ЃЌШчЙћЧЇЮЛгыЪЎЮЛЩЯЕФЪ§зжжЎКЭЮЊ7ЃЌАйЮЛгыИіЮЛЩЯЕФЪ§зжжЎКЭвВЮЊ7ЃЌФЧУДГЦ
ЃЌШчЙћЧЇЮЛгыЪЎЮЛЩЯЕФЪ§зжжЎКЭЮЊ7ЃЌАйЮЛгыИіЮЛЩЯЕФЪ§зжжЎКЭвВЮЊ7ЃЌФЧУДГЦ![]() ЮЊЁАЩЯНјЪ§ЁБЃЎ
ЮЊЁАЩЯНјЪ§ЁБЃЎ
(1)аДГізюаЁКЭзюДѓЕФЁАЩЯНјЪ§ЁБЃЛ
(2)вЛИіЁАЩЯНјЪ§ЁБ![]() ЃЌШє
ЃЌШє![]() ЃЌЧвЪЙвЛдЊЖўДЮЗНГЬ
ЃЌЧвЪЙвЛдЊЖўДЮЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓетИіЁАЩЯНјЪ§ЁБЃЎ
гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓетИіЁАЩЯНјЪ§ЁБЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкСтаЮABCDжаЃЌЁЯAЃН120ЁуЃЌЕуEЪЧBCБпЕФжаЕуЃЌЕуPЪЧЖдНЧЯпBDЩЯвЛЖЏЕуЃЌЩшPDЕФГЄЖШЮЊxЃЌPEгыPCЕФГЄЖШКЭЮЊyЃЌЭМ2ЪЧyЙигкxЕФКЏЪ§ЭМЯѓЃЌЦфжаHЪЧЭМЯѓЩЯЕФзюЕЭЕуЃЌдђa+bЕФжЕЮЊЃЈЁЁЁЁЃЉ
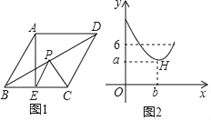
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЖдгкШЮвтШ§ЕуAЃЌBЃЌCЃЌИјГіШчЯТЖЈвхЃКШєОиаЮЕФШЮКЮвЛЬѕБпОљгыФГЬѕзјБъжсЦНааЛђжиКЯЃЌЧвAЃЌBЃЌCШ§ЕуЖМдкОиаЮЕФФкВПЛђБпНчЩЯЃЌдђГЦИУОиаЮЮЊЕуAЃЌBЃЌCЕФЭтбгОиаЮЃЌЕуAЃЌBЃЌCЕФЫљгаЭтбгОиаЮжаЃЌУцЛ§зюаЁЕФОиаЮГЦЮЊЕуAЃЌBЃЌCЕФзюМбЭтбгОиаЮЃЎР§ШчЃЌЭМЂйжаЕФОиаЮA1B1C1D1ЃЌA2B2C2D2ЃЌA3B3CD3ЃЌЖМЪЧЕуAЃЌBЃЌCЕФЭтбгОиаЮЃЌОиаЮA3B3CD3ЪЧЕуAЃЌBЃЌCЕФзюМбЭтбгОиаЮЃЎ
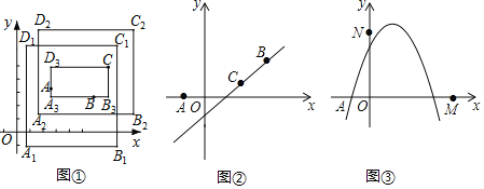
ЃЈ1ЃЉШчЭМЂкЃЌвбжЊAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ2ЃЉЃЌЕуCдкжБЯпyЃНxЉ1ЩЯЃЌЩшЕуCЕФКсзјБъЮЊtЃЎ
ЂйШєtЃН![]() ЃЌдђЕуAЃЌBЃЌCЕФзюМбЭтбгОиаЮЕФУцЛ§ЮЊЖрЩйЃП
ЃЌдђЕуAЃЌBЃЌCЕФзюМбЭтбгОиаЮЕФУцЛ§ЮЊЖрЩйЃП
ЂкШєЕуAЃЌBЃЌCЕФзюМбЭтбгОиаЮЕФУцЛ§ЮЊ9ЃЌЧѓtЕФжЕЃЎ
ЃЈ2ЃЉШчЭМЂлЃЌвбжЊЕуMЃЈ4ЃЌ0ЃЉЃЌNЃЈ0ЃЌ![]() ЃЉЃЌPЃЈxЃЌyЃЉЪЧХзЮяЯпyЃНЉx2+2x+3ЩЯвЛЕуЃЌЧѓЕуMЃЌNЃЌPЕФзюМбЭтбгОиаЮУцЛ§ЕФзюаЁжЕЃЌвдМАДЫЪБЕуPЕФКсзјБъxЕФШЁжЕЗЖЮЇЃЛ
ЃЉЃЌPЃЈxЃЌyЃЉЪЧХзЮяЯпyЃНЉx2+2x+3ЩЯвЛЕуЃЌЧѓЕуMЃЌNЃЌPЕФзюМбЭтбгОиаЮУцЛ§ЕФзюаЁжЕЃЌвдМАДЫЪБЕуPЕФКсзјБъxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉвбжЊDЃЈ1ЃЌ0ЃЉЃЎШєQЪЧХзЮяЯпyЃНЉx2Љ2mxЉm2+2m+1ЕФЭМЯѓдкЉ2ЁмxЁм1жЎМфЕФзюИпЕуЃЌЕуEЕФзјБъЮЊЃЈ0ЃЌ4mЃЉЃЌЩшЕуDЃЌEЃЌQЕФзюМбЭтбгОиаЮЕФУцЛ§ЮЊSЃЌЕБ4ЁмSЁм6ЪБЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCКЭЁїADEЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯBAC=ЁЯDAE=90ЁуЃЌЫФБпаЮACDEЪЧЦНааЫФБпаЮЃЌСЌНсCEНЛADгкЕуFЃЌСЌНсBDНЛCEгкЕуGЃЌСЌНсBE. ЯТСаНсТлжаЃКЂй CE=BDЃЛ ЂкЁїADCЪЧЕШбќжБНЧШ§НЧаЮЃЛ
ЂлЁЯADB=ЁЯAEBЃЛ Ђм CDЁЄAE=EFЁЄCGЃЛ
вЛЖЈе§ШЗЕФНсТлга
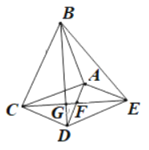
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаЫФеХБГУцЯрЭЌЕФжНХЦAЁЂBЁЂCЁЂDЃЌЦфе§УцЩЯЗНЗжБ№ЛгаЫФИіВЛЭЌЕФМИКЮЭМаЮЃЌЯТЗНаДгаЫФИіВЛЭЌЫуЪНЃЌаЁУїНЋЫФеХжНХЦБГУцГЏЩЯЯДдШКѓУўГівЛеХЃЌНЋЦфгр3еХЯДдШКѓдйУўГівЛеХЃЎ
(1)гУЪїзДЭМ(ЛђСаБэЗЈ)БэЪОСНДЮУўХЦЫљгаПЩФмГіЯжЕФНсЙћ(жНХЦгУAЁЂBЁЂCЁЂDБэЪО)ЃЛ
(2)ЧѓУўГіЕФСНеХжНХЦЕФЭМаЮЪЧжааФЖдГЦЭМаЮЧвЫуЪНвВе§ШЗЕФжНХЦЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com