
【题目】每个小正方形都是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系中的位置如图所示.
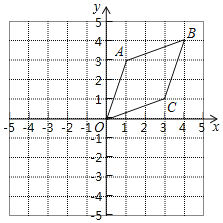
(1)画出菱形OABC关于原点O的中心对称图形OA1B1C1,并直接写出点B1的坐标;
(2)将菱形OABO绕原点O顺时针旋转90°,得到菱形OA2B2C2,请画出菱形OA2B2C2并求出点B旋转到B2的路径长.
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
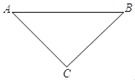
【题目】如图,在Rt△ABC中,AC=BC,AB=10,以AB为斜边向上作Rt△ABD,使∠ADB=90°.连接CD,若CD=7![]() ,则AD=_____.
,则AD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
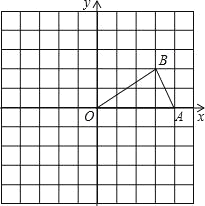
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,有下列结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中,正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
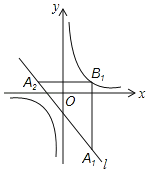
【题目】如图,在平面直角坐标系xOy中,已知直线l:y=﹣x﹣1,双曲线y=![]() ,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2018=_____;若要将上述操作无限次地进行下去,则a1不可能取的值是_____.
,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2018=_____;若要将上述操作无限次地进行下去,则a1不可能取的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D.
(1)求证: ![]() .
.
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即
![]() ,如T(60°)=1.
,如T(60°)=1.
①理解巩固:T(90°)= ________,T(120°)=_________,若α是等腰三角形的顶角,则T(α)的取值范围是_____________________;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点这沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1).
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
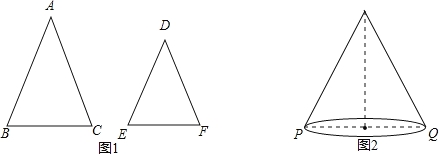
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com