
【题目】如图1,线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,连接AE,BD,分别交CD,CA于Q,P.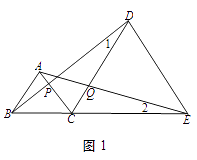
(1)找出图中的所有全等三角形.
(2)找出一组相等的线段,并说明理由.
(3)如图2,取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状,并说明理由.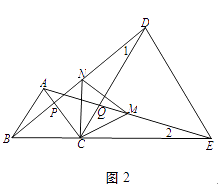
【答案】
(1)解:△BCD≌△ACE;△BPC≌△AQC;△DPC≌△EQC
(2)解:BD=AE.
理由:等边三角形ABC、DCE中,∵∠ACB=∠ACD=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中, 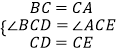 ,
,
∴△BCD≌△ACE(SAS),
∴BD=AE.
(3)解:等边三角形.
理由:由△BCD≌△ACE,
∴∠1=∠2,BD=AE.
∵M是AE的中点、N是BD的中点,
∴DN=EM,又DC=CE.
在△DCN和△ECM中, 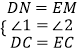 ,
,
∴△DCN≌△ECM(SAS),
∴CN=CM,∠NCD=∠MCE,∠MCE+∠DCM=60°.
∴∠NCD+∠DCM=60°,即∠NCM=60°,
又∵CM=CN,
∴△CMN为等边三角形
【解析】(1)先观察图形那些三角形是全等的,然后结合题中条件去推理;(2)由等边三角形的性质推出边相等、角相等,由“SAS”推出全等(3)由第(1)问去等推出△DCN≌△ECM,再证∠NCM=60°即得证.
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°. 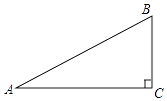
(1)用尺规在AC边上求作点D,使AD=BD;(保留痕迹,不写作法)
(2)若(1)中所得BD平分∠ABC,则∠A= . (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D.得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;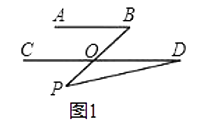
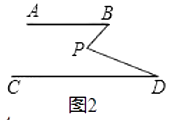
(2)在如图2中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明);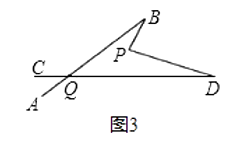
(3)根据(2)的结论求如图4中∠A+∠B+∠C+∠D+∠E的度数.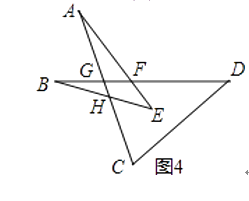
查看答案和解析>>
科目:初中数学 来源: 题型:
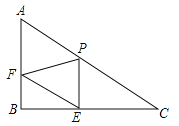
【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=8,∠BAC=110°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E.则△ADE的周长为;∠DAE的度数为 . 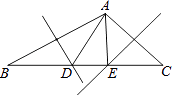
查看答案和解析>>
科目:初中数学 来源: 题型:
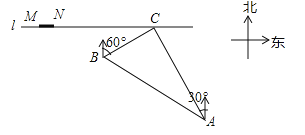
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.以轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断中正确的是( )
A.对角线互相垂直的四边形是菱形
B.三个角相等的四边形是矩形
C.对角线相等的平行四边形是正方形
D.对角线互相平分垂直且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校将周五上午大课间活动项目定为跳绳活动,为此学校准备购置长、短两种跳绳若干.已知长跳绳的单价比短跳绳单价的三倍少4元,且购买2条长跳绳与购买5条短跳绳的费用相同.
(1)两种跳绳的单价各是多少元?
(2)若学校准备用不超过1950元的现金购买190条长、短跳绳,且短跳绳的条数不超过长跳绳的5倍,问学校有几种购买方案可供选择?并写出这几种方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com