
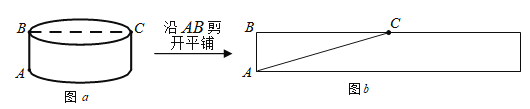
����Ŀ����ͼ![]() ��Բ���ĵ���뾶Ϊ
��Բ���ĵ���뾶Ϊ![]() ��Բ����
��Բ����![]() Ϊ
Ϊ![]() ��
��![]() �ǵ���ֱ������һֻ���ϴӵ�
�ǵ���ֱ������һֻ���ϴӵ�![]() ������Բ���������е���
������Բ���������е���![]() �����·�ߣ�С�����������·�ߣ�
�����·�ߣ�С�����������·�ߣ�
·��1������![]() ����ֱ��
����ֱ��![]() ����ͼ
����ͼ![]() ��ʾ���賤��Ϊ
��ʾ���賤��Ϊ![]() ��
��
·��2������չ��ͼ�е��߶�![]() ����ͼ
����ͼ![]() ��ʾ���賤��Ϊ
��ʾ���賤��Ϊ![]() ��
��
�밴��С����˼·�������������̣�
��1���⣺![]()
![]() ��
��
![]()
��2��С��������������Щ�ɻ��������������ijɣ���Բ������뾶Ϊ![]() ����
����![]() Ϊ
Ϊ![]() ��������ǰ���·�߽��м��㣮���������
��������ǰ���·�߽��м��㣮���������![]() ��
��
�ٴ�ʱ��·��1��__________��·��2��_____________��
������ѡ������·�߽϶̣���˵�����ɣ�
���𰸡���1������������2����![]() ��
�� ![]() ����ѡ��·��2�϶̣����ɼ�������
����ѡ��·��2�϶̣����ɼ�������
��������
��1�����ݹ��ɶ�����·��1��l12=AC2=��2+�����ܳ�һ��2��·��2��l22=����+����ֱ����2��������ƽ���Ƚϣ�ƽ����ģ������ʹ�
��2����l1�ij��ȵ���AB�ij�����BC�ij��ȵĺͣ�l2�ij��ȵ�ƽ������AB�ij��ȵ�ƽ��������ܳ���һ���ƽ���ĺͣ��ݴ����l2�ij��ȼ��ɣ�
�ڱȽϳ�l12��l22�Ĵ�С��ϵ�������Ƚϳ�l1��l2�Ĵ�С��ϵ���жϳ�ѡ������·�߽϶̼���
��1��![]()
![]() ;
;
![]()
![]()
![]()
![]()
��![]()
����ѡ��·��1�϶̣�
��2����l1=4+2��2=8��
![]() ��
��
��![]() ��
��
![]() ��
��![]()
����ѡ��·��2�϶̣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ��������![]() ��
��![]() �����������㣬��ô�Ը������ߵĶ��������������Ϊ����������γ�Ϊ���������ߵġ������������Ρ���
�����������㣬��ô�Ը������ߵĶ��������������Ϊ����������γ�Ϊ���������ߵġ������������Ρ���
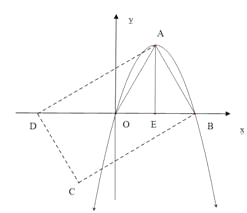
��1���������������Ρ�һ���� �����Σ�
��2����������![]() �ġ������������Ρ��ǵ���ֱ�������Σ���
�ġ������������Ρ��ǵ���ֱ�������Σ���![]() ��ֵ��
��ֵ��
��3����ͼ����![]() ��������
��������![]() �ġ������������Ρ����Ƿ������ԭ��
�ġ������������Ρ����Ƿ������ԭ��![]() Ϊ�Գ����ĵľ���
Ϊ�Գ����ĵľ���![]() �������ڣ������
�������ڣ������![]() ����������ߵı���ʽ���������ڣ�˵�����ɣ�
����������ߵı���ʽ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ﻪС��ͣ����ȥ���շѱ����£�����������ͣ����Ϊ600Ԫ/����С��������ͣ����Ϊ400Ԫ/����ͣ������ʱ����ͣ����23000Ԫ�������շѱ��ϵ�Ϊ������������ͣ����Ϊ1000Ԫ/����С��������ͣ����Ϊ600Ԫ/��������С��ͣ�������ɵij�����û�б仯�������ȥ�����ȡͣ����13000Ԫ.
��1����ͣ����ȥ����ͣ�С�С����������������
��2�������С��������Ҫ��С��ͣ�����������ͣ������������11�������ͣ����������ͣ��������![]() ����С��������
����С��������![]() ����ͣ������ȡ����ͣ����Ϊ
����ͣ������ȡ����ͣ����Ϊ![]() Ԫ�������
Ԫ�������![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��3���ڣ�2���������£��������ͣ����ͣ������ʱС����������������������������2����������ͣ������������ȡ��ͣ���ѹ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���y=��x2+![]() x+c��x�ύ�ڵ�M��x1��0��N��x2��0�����㣬��y�ύ�ڵ�H��
x+c��x�ύ�ڵ�M��x1��0��N��x2��0�����㣬��y�ύ�ڵ�H��
��1������HMO=45�㣬��MHN=105��ʱ����������ʽ��
��2����|x1|2+|x2|2=1������Q��b��c����ֱ��![]() ��ʱ������κ���y=��x2+
��ʱ������κ���y=��x2+![]() x+c�Ľ���ʽ��
x+c�Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90����AC=6��BC=8.
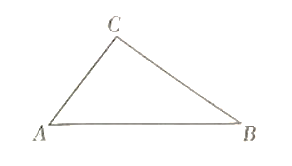
��1����ֱ�ߺ�Բ������A��ƽ���ߣ���BC�ڵ�D����Ҫ��д������������ͼ�ۼ���
��2����S��ADC: S��ADB��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ��������__________��
��������__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ٹ�·��![]() ��·����Ҫά�ޣ��ⰲ�żס����������̶Ӻ�����ɣ��涨���ڲ��ó���һ����(30��) ����֪��ÿ��ά��·�ij������Ҷ�ÿ��ά��·���ȵ�2���������ڸ��Զ�����ɳ���Ϊ
��·����Ҫά�ޣ��ⰲ�żס����������̶Ӻ�����ɣ��涨���ڲ��ó���һ����(30��) ����֪��ÿ��ά��·�ij������Ҷ�ÿ��ά��·���ȵ�2���������ڸ��Զ�����ɳ���Ϊ![]() ��·��ά��ʱ���ӱ��Ҷ�����6��
��·��ά��ʱ���ӱ��Ҷ�����6��
��1������������̶�ÿ�������ά��·�ij��ȷֱ��Ƕ���![]()
��2�����ӵĹ��̷���Ϊÿ��2��Ԫ���Ҷ�ÿ��Ĺ��̷���Ϊ1.2��Ԫ��15 ����Ҷ������������¹����ɼ���ɣ������ж��ܷ��ڹ涨�Ĺ���������ܷ��ò�����80��Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
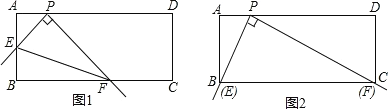
����Ŀ���ھ��� ABCD ������ P �� AD ����AB= ![]() ��AP=1����ֱ�dzߵĶ������ P ����ֱ�dzߵ����߷ֱ� AB��BC �ڵ� E��F������ EF����ͼ 1�������� E ��� B �غ�ʱ���� F ǡ����� C �غϣ��� ͼ 2��.��ֱ�dzߴ�ͼ 2 �е�λ�ÿ�ʼ���Ƶ� P ˳ʱ����ת������ E �͵� A �غ�ʱֹͣ����������� �У��ӿ�ʼ��ֹͣ���߶� EF ���е���������·����Ϊ__________ ��
��AP=1����ֱ�dzߵĶ������ P ����ֱ�dzߵ����߷ֱ� AB��BC �ڵ� E��F������ EF����ͼ 1�������� E ��� B �غ�ʱ���� F ǡ����� C �غϣ��� ͼ 2��.��ֱ�dzߴ�ͼ 2 �е�λ�ÿ�ʼ���Ƶ� P ˳ʱ����ת������ E �͵� A �غ�ʱֹͣ����������� �У��ӿ�ʼ��ֹͣ���߶� EF ���е���������·����Ϊ__________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̼�����ɫ�����������dz�����һ�����ʽ���йز��ŵ�����ij��λԱ�����°�Ľ�ͨ��ʽ������������ͳ��ͼ��

��1����գ����ε����������Ϊ�� ���ˣ���˽�ҳ�������m���� ��������ͳ��ͼ���������г����������ε�Բ�Ľ�Ϊ�� ���ȣ�
��2����ȫ����ͳ��ͼ��
��3�����õ�λ����2000�ˣ������õ�λ�����г����°��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com