
【题目】在数学课上,老师提出如下问题:如何使用尺规完成“过直线l外一点P作已知直线l的平行线”.
小明的作法如下:
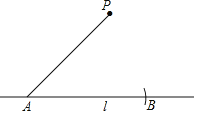
①在直线l上取一点A,以点A为圆心,AP长为半径作弧,交直线l于点B;
②分别以P,B为圆心,以AP长为半径作弧,两弧相交于点Q(与点A不重合);
③作直线PQ.所以直线PQ就是所求作的直线.根据小明的作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB=AP= = .
∴四边形ABQP是菱形( )(填推理的依据).
∴PQ∥l.
科目:初中数学 来源: 题型:
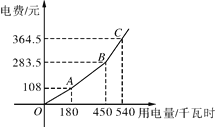
【题目】为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如图的折线图,请根据图象回答下列问题;
(1)当用电量是180千瓦时时,电费是__________元;
(2)第二档的用电量范围是__________;
(3)“基本电价”是__________元/千瓦时;
(4)小明家8月份的电费是328.5元,这个月他家用电多少千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
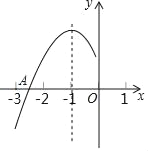
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2<﹣1,则y1>y2,⑤abc>0.其中正确结论的个数是( )
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下图,解答下列问题.

(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,那么第八层有几个小圆圈?第n层呢?
(2)某一层上有65个圆圈,这是第几层?
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3=22.同样,
由前三层的圆圈个数和得:1+3+5=32.
由前四层的圆圈个数和得:1+3+5+7=42.
由前五层的圆圈个数和得:1+3+5+7+9=52.…
根据上述请你计算:1+3+5+…+99的和
(4)猜测:从1开始的n个连续奇数之和是多少?用公式把它表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等等.
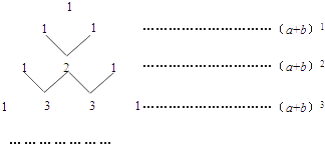
(1)根据上面的规律,则(a+b)5的展开式=________.
(2)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为6,BC=4,AB=12.
(1)求点A、B对应的数;
(2)动点P、Q分别同时从A、C出发,分别以每秒6个单位和3个单位的速度沿数轴正方向运动.M为AP的中点,N在CQ上,且CN=![]() CQ,设运动时间为t(t>0).
CQ,设运动时间为t(t>0).
①求点M、N对应的数(用含t的式子表示); ②t为何值时,OM=2BN.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
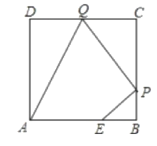
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7,9,…,排列成如图所示的数表:
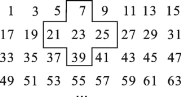
(1)十字框中的五个数的和与中间数23有什么关系?
(2)设中间数为![]() ,用式子表示十字框中五个数之和.
,用式子表示十字框中五个数之和.
(3)将十字框上、下、左、右平移,可框住另外五个数,这五个数还有这种规律吗?
(4)十字框中的五个数之和能等于2015吗?若能,请写出这五个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为两人对抗赛,即把四种比赛项目写在4张完全相同的卡片上,比赛时,比赛的两人从中随机抽取1张卡片作为自己的比赛项目(不放回,且每人只能抽取一次)比赛时,小红和小明分到一组.(1)小明先抽取,那么小明抽到唐诗的概率是多少?
(2)小红擅长唐诗,小红想:“小明先抽取,我后抽取”抽到唐诗的概率是不同的,且小明抽到唐诗的概率更大,若小红后抽取,小红抽中唐诗的概率是多少?小红的想法对吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com