
【题目】如图所示,在△ABC中,AB=AC=![]() ,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
(1)求作圆O(尺规作图,保留作留痕迹,不写作法);
(2)求证:AC是OO的切线;
(3)若点P为圆O上一点,且弧PA=弧PB,连接PC,求线段PC的长.
【答案】(1)如图所示即为答案;(2)详见解析;(3)![]() 或2
或2![]()
【解析】
(1)根据外心的定义即可求作圆O;
(2)根据切线的判定即可证明AC是⊙O的切线;
(3)根据点P为圆O上一点,且弧PA=弧PB,连接PC,即可求线段PC的长.
解:(1)如图,圆O即为所求;
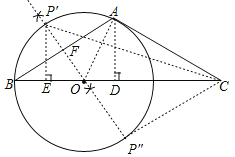
(2)证明:连接OA,
∵OA=OB,
∴∠OAB=∠B=30°,
∵AB=AC,
∴∠ACB=∠B=30°,
∴∠BAC=120°,
∴∠CAO=∠BAC﹣∠OAB=90°,
∴OA⊥AC,OA是⊙O的半径,
∴AC是⊙O的切线;
(3)∵弧PA=弧PB,
∴符合条件的点P有两个,P′和P″,连接P′C和P″C,
作P′E⊥BC于点E,
∵OP′⊥AB,
根据垂径定理,得
AF=BF=![]() AB=
AB=![]() ,
,
∵∠B=30,
∴∠P′OB=60°,
∴OB=![]() ,
,
∴P′E=BF=![]() ,
,
BE=![]() OB=
OB=![]() ,
,
∵AB=AC=2![]() ,
,
作AD⊥BC于点D,则AD=![]() ,DC=
,DC=![]() ,
,
∴BC=2DC=2![]() ,
,
∴CE=BC﹣BE=![]() ,
,
∴P′C=![]() ;
;
连接P″C,
∵OA=OP″,∠AOC=∠COP″=60°,OC=OC,
∴△AOC≌△P″OC(SAS),
∴P″C=AC=2![]() .
.
综上所述:线段PC的长为![]() 或2
或2![]() .
.


科目:初中数学 来源: 题型:
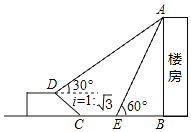
【题目】如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房顶部A的仰角为30°,沿坡面向下走到坡脚C处,然后在地面上沿CB向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为60°.已知坡面CD=10米,山坡的坡度i=1:![]() (坡度是指坡面的铅直高度与水平宽度的比).求楼房AB高度.(结果保留根式)
(坡度是指坡面的铅直高度与水平宽度的比).求楼房AB高度.(结果保留根式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个直角三角形的三边长分别为![]() ,则称这个三角形均匀直角三角形.
,则称这个三角形均匀直角三角形.
(1)判定按照上述定义,下列长度的三条线段能组成均匀直角三角形的是()
A.1,2,3 B.1,1,2 C.2,3,4 D.3,4,5,
(2)性质求证:任何均匀直角三角形的较小直角边与较大直角边的比是![]()
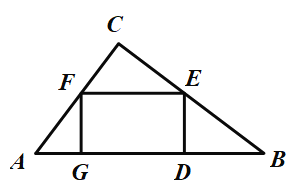
(3)应用如图,在一块均匀直角三角形纸板![]() 中剪一个矩形,且矩形的一边在
中剪一个矩形,且矩形的一边在![]() 上,其余两个顶点分别在
上,其余两个顶点分别在![]() 上,已知
上,已知![]() ,求剪出矩形面积的最大值.
,求剪出矩形面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②3a+c>0;
③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
④当y>3时,x的取值范围是0≤x<2;
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
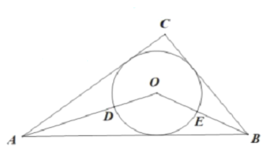
【题目】如图,在Rt![]() ABC中,∠C=90
ABC中,∠C=90![]() ,AC=8,BC=6,
,AC=8,BC=6,![]() O为ABC的内切圆,OA,OB与
O为ABC的内切圆,OA,OB与![]() O分别交于点D,E,则劣弧DE的长是________.
O分别交于点D,E,则劣弧DE的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
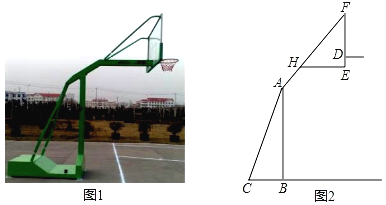
【题目】如图1、图2是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮筐D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮筐D到地面的距离.(精确到0.1米,参考数据:cos75°≈0.3,sin75°≈0.9,tan75°≈3.7,![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
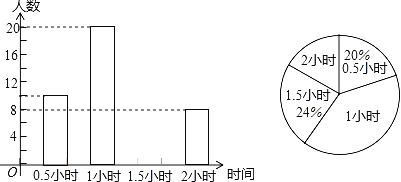
(1)在这次调查中共调查了多少名学生;
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)求户外活动时间的众数和中位数是多少;
(4)本次调查中学生参加户外活动的平均时间是否符合要求,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为![]() 元/个的粽子,根据市场预测,该品牌粽子每个售价
元/个的粽子,根据市场预测,该品牌粽子每个售价![]() 元时,每天能出售
元时,每天能出售![]() 个,并且售价每上涨
个,并且售价每上涨![]() 元,其销售量将减少
元,其销售量将减少![]() 个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的
个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的![]() .
.
(1)请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为![]() 元.
元.
(2)定价为多少时每天的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+2x﹣3与x轴交于A,B两点(点A在点B的左侧),将这条抛物线向右平移m(m>0)个单位长度,平移后的抛物线与x轴交于C,D两点(点C在点D的左侧),若B,C是线段AD的三等分点,则m的值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com