
【题目】如图,在Rt![]() ABC中,∠C=90
ABC中,∠C=90![]() ,AC=8,BC=6,
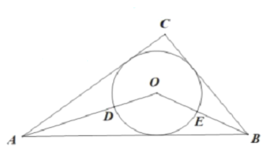
,AC=8,BC=6,![]() O为ABC的内切圆,OA,OB与
O为ABC的内切圆,OA,OB与![]() O分别交于点D,E,则劣弧DE的长是________.
O分别交于点D,E,则劣弧DE的长是________.
【答案】![]()
【解析】
作OF⊥AC于点F,OG⊥BC于点G,OH⊥AB于点H,得到四边形CFOG是矩形,根据切线长定理得到圆O的半径,再根据角平分线得到劣弧DE所对的圆心角,最后根据弧长的计算公式即可解答.
解:如图,作OF⊥AC于点F,OG⊥BC于点G,OH⊥AB于点H,
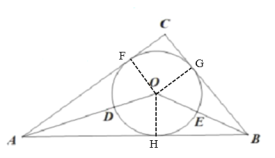
设圆O的半径为r,
则四边形CFOG是矩形,
在Rt△ABC中,∵∠C=90![]() ,AC=8,BC=6,
,AC=8,BC=6,
∴AB=![]() ,
,
∵![]() O为ABC的内切圆,
O为ABC的内切圆,
∴OF=OG,
∴矩形CFOG是正方形,
∴CF=CG=r,
则AF=AH=8-r,BG=BH=6-r,
∴AH+BH=8-r+6-r=10,解得:r=2,
又∵![]() O为ABC的内切圆,
O为ABC的内切圆,
∴OA,OB分别平分∠CAB、∠ABC,
∴∠OAB=![]() ∠CAB,∠OBA=
∠CAB,∠OBA=![]() ∠ABC,
∠ABC,
∵∠C=90°,
∴∠OAB+∠OBA=![]() (∠CAB+∠ABC)=
(∠CAB+∠ABC)=![]() ×90°=45°,
×90°=45°,
∴∠DOE=180°-(∠OAB+∠OBA)=135°,
∴劣弧DE的长是:![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,P是线段BC上任意一点,以点P为圆心PB为半径的圆与线段AB相交于点Q(点Q与点A、B不重合),∠CPQ的角平分线与AC相交于点D.
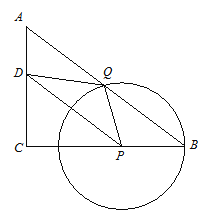
(1)如果DQ=PB,求证:四边形BQDP是平行四边形;
(2)设PB=x,△DPQ的面积为y,求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ADQ是以DQ为腰的等腰三角形,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果一个图形向右平移1个单位,再向上平移3个单位,称为一个变换,已知点![]() ,经过一个变换后对应点为
,经过一个变换后对应点为![]() ,经过2个变换后对应点为
,经过2个变换后对应点为![]() ,经过
,经过![]() 个变换后对应点为
个变换后对应点为![]() ,则用含
,则用含![]() 的代数式教示点
的代数式教示点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课余生活,引领学生多读书、会读书、读好书,重庆一中聘请了西南师大教授讲授“诗歌赏析”.为激励学生积极参与,凡听课者每人发了一张带号码的入场券,授课结束后将进行抽奖活动.设立一等奖一名,获100元购书卡,二等奖3名分别获50元购书卡,三等奖6名分别获价值20元的书一本,纪念奖若干分别获价值2元的笔一支.工作人员对听课学生人数情况进行了统计,绘制了如下统计图:
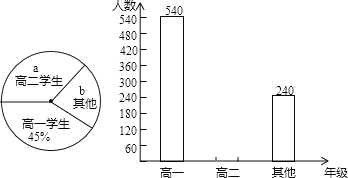
请根据以上信息解答下列问题
(1)这次授课共 名学生参加,扇形图中的a= ,b= ;
(2)补全条形统计图;
(3)学校共花费570元设奖,则本次活动中奖的概率是多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC=![]() ,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
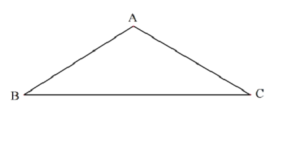
(1)求作圆O(尺规作图,保留作留痕迹,不写作法);
(2)求证:AC是OO的切线;
(3)若点P为圆O上一点,且弧PA=弧PB,连接PC,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求线段BC的长;
(2)当0≤y≤3时,请直接写出x的范围;
(3)点P是抛物线上位于第一象限的一个动点,连接CP,当∠BCP=90o时,求点P的坐标.
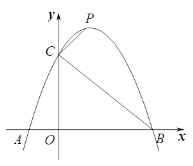
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com