
ЁОЬтФПЁПЮЊЗсИЛбЇЩњПЮгрЩњЛюЃЌв§СьбЇЩњЖрЖСЪщЁЂЛсЖСЪщЁЂЖСКУЪщЃЌжиЧьвЛжаЦИЧыСЫЮїФЯЪІДѓНЬЪкНВЪкЁАЪЋИшЩЭЮіЁБЃЎЮЊМЄРјбЇЩњЛ§МЋВЮгыЃЌЗВЬ§ПЮепУПШЫЗЂСЫвЛеХДјКХТыЕФШыГЁШЏЃЌЪкПЮНсЪјКѓНЋНјааГщНБЛюЖЏЃЎЩшСЂвЛЕШНБвЛУћЃЌЛё100дЊЙКЪщПЈЃЌЖўЕШНБ3УћЗжБ№Лё50дЊЙКЪщПЈЃЌШ§ЕШНБ6УћЗжБ№ЛёМлжЕ20дЊЕФЪщвЛБОЃЌМЭФюНБШєИЩЗжБ№ЛёМлжЕ2дЊЕФБЪвЛжЇЃЎЙЄзїШЫдБЖдЬ§ПЮбЇЩњШЫЪ§ЧщПіНјааСЫЭГМЦЃЌЛцжЦСЫШчЯТЭГМЦЭМЃК
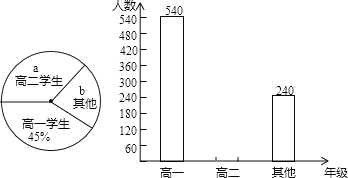
ЧыИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬт
ЃЈ1ЃЉетДЮЪкПЮЙВЁЁ ЁЁУћбЇЩњВЮМгЃЌЩШаЮЭМжаЕФaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉбЇаЃЙВЛЈЗб570дЊЩшНБЃЌдђБОДЮЛюЖЏжаНБЕФИХТЪЪЧЖрДѓЃП
ЁОД№АИЁПЃЈ1ЃЉ1200ЃЌ35%ЃЌ20%ЃЎЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЃЌНсКЯЩШаЮЭМгыЬѕаЮЭМПЩЕУИпвЛга540ШЫВЮМгЃЌеМ45%ЃЌПЩЕУВЮМгЬ§ПЮЕФзмШЫЪ§ЃЌНјЖјПЩЕУИпШ§бЇЩњеМЕФАйЗжБШЃЌдйИљОнИїВПЗжЕФАйЗжБШжЎКЭЮЊ1ЃЌПЩЕУИпЖўЕФБШР§ЃЛ
ЃЈ2ЃЉгаЃЈ1ЃЉЕФНсТлЃЌПЩЕУИпЖўЕФШЫЪ§ЃЌОнДЫПЩвдВЙШЋЬѕаЮЭМЃЛ
ЃЈ3ЃЉИљОнЬтвтЃЌЩшга1ИівЛЕШНБЃЌ3ИіЖўЕШНБЃЌ6ИіШ§ЕШНБЃЌmИіМЭФюНБЃЌдђПЩЕУЦфЙиЯЕЪНЃЌНтПЩЕУmЕФжЕЃЌНјЖјПЩЕУД№АИЃЎ
ЃЈ1ЃЉИљОнЬтвтЃЌНсКЯЩШаЮЭМгыЬѕаЮЭМПЩЕУИпвЛга540ШЫВЮМгЃЌеМ45%ЃЌПЩЕУЙВга540ЁТ45%ЃН1200ШЫЃЌ
НјЖјПЩЕУЃЌИпШ§га240ЁТ1200ЁС100%ЃН20%ЃЌ
ИпЖўеМ1Љ45%Љ20%ЃН35%ЃЛ
ЙЪД№АИЮЊ1200ЃЌ35%ЃЌ20%ЃЎ
ЃЈ2ЃЉ
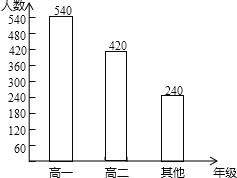
ЃЈ3ЃЉЩшга1ИівЛЕШНБЃЌ3ИіЖўЕШНБЃЌ6ИіШ§ЕШНБЃЌmИіМЭФюНБЃЌ
дђЃК100+3ЁС50+20ЁС6+m2ЃН570
2mЃН200
mЃН100
ЁрБОДЮЛюЖЏжаНБЕФИХТЪЮЊЃК![]()


 ПЊаФЭмзДдЊВтЪдОэЯЕСаД№АИ
ПЊаФЭмзДдЊВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫФБпаЮABCDжаЃЌЖдНЧЯпACЁЂBDЯрЛЅДЙжБЃЌAC=4ЃЌBD=6ЃЌЫГДЮСЊНсетИіЫФБпаЮжаЕуЫљЕУЕФЫФБпаЮЕФУцЛ§ЕШгк________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌвд
жаЃЌвд![]() ЮЊжБОЖЕФ
ЮЊжБОЖЕФ![]() НЛ
НЛ![]() БпгкЕу
БпгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌСЌНс
ЃЌСЌНс![]()
ЃЈ1ЃЉЧѓжЄЃК![]()
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжБОЖЃЎ
ЕФжБОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
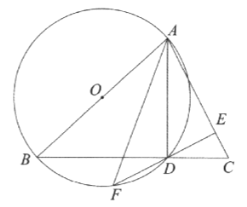
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЖўДЮКЏЪ§yЃНax2Љ4ax+3ЕФЭМЯѓгыxжсе§АыжсНЛгкЕуAЁЂBЃЌгыyжсЯрНЛгкЕуCЃЌЖЅЕуЮЊDЃЌЧвtanЁЯCAOЃН3ЃЎ
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧЖдГЦжсгвВрХзЮяЯпЩЯЕФЕуЃЌСЊНсCPЃЌНЛЖдГЦжсгкЕуFЃЌЕБSЁїCDFЃКSЁїFDPЃН2ЃК3ЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЁїPCDбижБЯпMNЗелЃЌЕБЕуPЧЁКУгыЕуOжиКЯЪБЃЌелКлMNНЛxжсгкЕуMЃЌНЛyжсгкЕуNЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
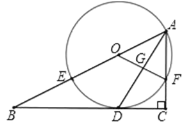
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌADЦНЗжЁЯBACНЛBCгкЕуDЃЌOЮЊABЩЯвЛЕуЃЌОЙ§ЕуAЃЌDЕФЁбOЗжБ№НЛABЃЌACгкЕуEЃЌFЃЌСЌНгOFНЛADгкЕуGЃЎ
(1)ЧѓжЄЃКBCЪЧЁбOЕФЧаЯпЃЛ
(2)ЧѓжЄЃК![]() ЃЛ
ЃЛ
(3)ШєBE=8ЃЌsinB=![]() ЃЌЧѓADЕФГЄЃЌ
ЃЌЧѓADЕФГЄЃЌ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
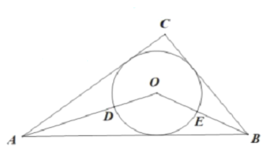
ЁОЬтФПЁПШчЭМЃЌдкRt![]() ABCжаЃЌЁЯC=90
ABCжаЃЌЁЯC=90![]() ЃЌAC=8ЃЌBC=6ЃЌ
ЃЌAC=8ЃЌBC=6ЃЌ![]() OЮЊABCЕФФкЧадВЃЌOAЃЌOBгы
OЮЊABCЕФФкЧадВЃЌOAЃЌOBгы![]() OЗжБ№НЛгкЕуDЃЌEЃЌдђСгЛЁDEЕФГЄЪЧ________ЃЎ
OЗжБ№НЛгкЕуDЃЌEЃЌдђСгЛЁDEЕФГЄЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌABCDЮЊЦНааЫФБпаЮЃЌAD=13ЃЌAB=25ЃЌЁЯDAB=ІСЃЌЧвcosa=![]() ЃЌЕуEЮЊжБЯпCDЩЯвЛЖЏЕуЃЌНЋЯпЖЮEAШЦЕуEФцЪБеыа§зЊІСЕУЕНЯпЖЮEFЃЌСЌНгCFЃЎ
ЃЌЕуEЮЊжБЯпCDЩЯвЛЖЏЕуЃЌНЋЯпЖЮEAШЦЕуEФцЪБеыа§зЊІСЕУЕНЯпЖЮEFЃЌСЌНгCFЃЎ
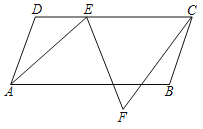
ЃЈ1ЃЉЧѓЦНааЫФБпаЮABCDЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕБЕуCЁЂBЁЂFШ§ЕуЙВЯпЪБЃЌЩшEFгыABЯрНЛгкЕуG,ЧѓЯпЖЮBGЕФГЄЃЛ
ЃЈ3ЃЉЧѓЯпЖЮCFЕФГЄЖШЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(1)ЯШЛЏМђЃЌдйЧѓжЕЃК(aЉ9+![]() )ЁТ(aЉ1Љ
)ЁТ(aЉ1Љ![]() )ЃЌЦфжаa=
)ЃЌЦфжаa=![]() ЃЛ
ЃЛ
(2)![]() Љ2cos30Ёу+(
Љ2cos30Ёу+(![]() )Љ2Љ
)Љ2Љ![]() ЃЛ
ЃЛ
(3)НтЗНГЬЃК![]() =1ЃЎ
=1ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
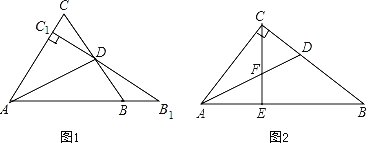
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЫљЪОЃКЕШБпЁїABCжаЃЌЯпЖЮADЮЊЦфФкНЧНЧЦНЗжЯпЃЌЙ§DЕуЕФжБЯпB1C1ЁЭACгкC1НЛABЕФбгГЄЯпгкB1ЃЎ
ЃЈ1ЃЉЧыФуЬНОПЃК![]() ЃЌ
ЃЌ![]() ЪЧЗёЖМГЩСЂЃП
ЪЧЗёЖМГЩСЂЃП
ЃЈ2ЃЉЧыФуМЬајЬНОПЃКШєЁїABCЮЊШЮвтШ§НЧаЮЃЌЯпЖЮADЮЊЦфФкНЧНЧЦНЗжЯпЃЌЧыЮЪ![]() вЛЖЈГЩСЂТ№ЃПВЂжЄУїФуЕФХаЖЯЃЎ
вЛЖЈГЩСЂТ№ЃПВЂжЄУїФуЕФХаЖЯЃЎ
ЃЈ3ЃЉШчЭМЃЈ2ЃЉЫљЪОRtЁїABCжаЃЌЁЯACBЃН90ЃЌACЃН8ЃЌBCЃН![]() ЃЌDEЁЮACНЛABгкЕуEЃЌЪдЧѓ
ЃЌDEЁЮACНЛABгкЕуEЃЌЪдЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com