
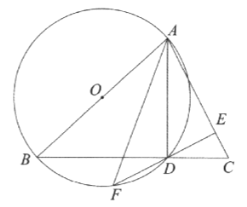
【题目】如图,在![]() 中,以
中,以![]() 为直径的
为直径的![]() 交
交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]()
(1)求证:![]()
(2)当![]() 时,求
时,求![]() 的直径.
的直径.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用直径所对的角是直角求得∠BDA=90°,由∠B=∠F,利用等角的余角相等,证得∠BAD=∠FAE,从而证得结论;
(2)连结BF,利用勾股定理求得AC=![]() ,再证得△ABF∽△ACD,得到
,再证得△ABF∽△ACD,得到![]() ,即可求解.
,即可求解.
(1)∵AB是圆O的直径,
∴∠BDA=90°,
∴∠BAD+∠B=90°,
∵EF⊥AC,
∴∠FAE+∠F=90°,
∵∠B=∠F,
∴∠BAD=∠FAE,
∴∠BAD-∠DAF=∠FAE-∠DAF,
即:∠BAF=∠DAC;
(2)连结BF,
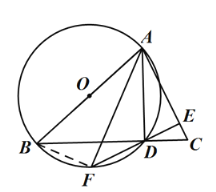
∵AB是圆O的直径,
∴∠BFA=90°,
∵∠BDA=90°,
∴∠ADC=180°-∠BDA=90°,
∴AC=![]() ,
,
∴∠BFA=∠ADC=90°,
由(1)得:∠BAF=∠DAC,
∴△ABF∽△ACD,
∴![]() ,即
,即![]() ,
,
∴![]() .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点A(2,m),B(-2,3m)分别在反比例函数![]() 和
和![]() 的图象上,经过点A、B的直线与y轴相交于点C.
的图象上,经过点A、B的直线与y轴相交于点C.
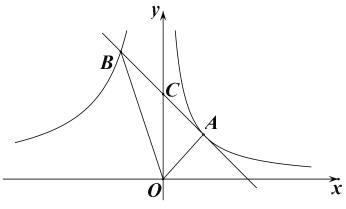
(1)求m和k的值;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面改善公园环境,现招标建设某全长960米绿化带,A,B两个工程队的竞标,A队平均每天绿化长度是B队的2倍,若由一个工程队单独完成绿装化,B队比A队要多用6天.
(1)分别求出A,B两队平均每天绿化长度.
(2)若决定由两个工程队共同合作绿化,要求至多4天完成绿化任务,两队都按(1)中的工作效率绿化完2天时,现又多出180米需要绿化,为了不超过4天时限,两队决定从第3天开始,各自都提高工作效率,且A队平均每天绿化长度仍是B队的2倍,则B队提高工作效率后平均每天至少绿化多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
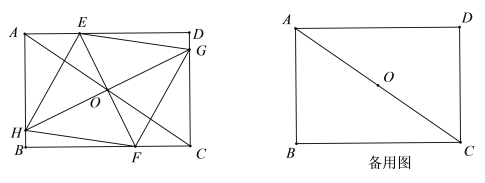
【题目】如图,E,F分别是边长为2cm的正方形ABCD的边AD,CD上的动点,满足AE=DF,连接BE,AF交于G,连接DG,则DG的最小值是_____.
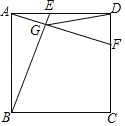
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果一个图形向右平移1个单位,再向上平移3个单位,称为一个变换,已知点![]() ,经过一个变换后对应点为
,经过一个变换后对应点为![]() ,经过2个变换后对应点为
,经过2个变换后对应点为![]() ,经过
,经过![]() 个变换后对应点为
个变换后对应点为![]() ,则用含
,则用含![]() 的代数式教示点
的代数式教示点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 是
是![]() 边上的动点,连接
边上的动点,连接![]() 并延长交于
并延长交于![]() 点
点![]() ,过
,过![]() 作
作![]() ,分别交矩形的边于点
,分别交矩形的边于点![]()
(1)当![]() 四点分别分布在矩形
四点分别分布在矩形![]() 的四条边上(不包括顶点)时,
的四条边上(不包括顶点)时,
①求证:四边形![]() 是菱形.
是菱形.
②求![]() 的取值范围.
的取值范围.
(2)当四边形![]() 的面积为144时,求
的面积为144时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课余生活,引领学生多读书、会读书、读好书,重庆一中聘请了西南师大教授讲授“诗歌赏析”.为激励学生积极参与,凡听课者每人发了一张带号码的入场券,授课结束后将进行抽奖活动.设立一等奖一名,获100元购书卡,二等奖3名分别获50元购书卡,三等奖6名分别获价值20元的书一本,纪念奖若干分别获价值2元的笔一支.工作人员对听课学生人数情况进行了统计,绘制了如下统计图:
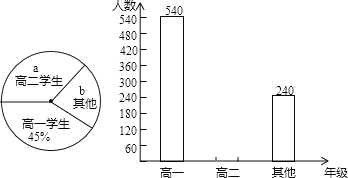
请根据以上信息解答下列问题
(1)这次授课共 名学生参加,扇形图中的a= ,b= ;
(2)补全条形统计图;
(3)学校共花费570元设奖,则本次活动中奖的概率是多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆心在坐标原点的⊙O,与坐标轴的交点分别为A、B和C、D.弦CM交OA于P,连结AM,已知tan∠PCO=![]() ,PC、PM是方程x2﹣px+20=0的两根.
,PC、PM是方程x2﹣px+20=0的两根.
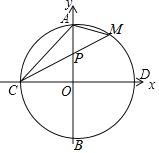
(1)求C点的坐标;
(2)写出直线CM的函数解析式;
(3)求△AMC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com