
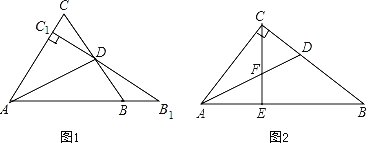
【题目】如图(1)所示:等边△ABC中,线段AD为其内角角平分线,过D点的直线B1C1⊥AC于C1交AB的延长线于B1.
(1)请你探究:![]() ,
,![]() 是否都成立?
是否都成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
(3)如图(2)所示Rt△ABC中,∠ACB=90,AC=8,BC=![]() ,DE∥AC交AB于点E,试求
,DE∥AC交AB于点E,试求![]() 的值.
的值.
【答案】(1)成立,理由见解析;(2)成立,理由见解析;(3)![]()
【解析】
(1)根据等边三角形的性质得到AD垂直平分BC,∠CAD=∠BAD=30°,AB=AC,则DB=CD,易得![]() ;由于∠C1AB1=60°,得∠B1=30°,则AB1=2AC1,同理可得到DB1=2DC1,易得
;由于∠C1AB1=60°,得∠B1=30°,则AB1=2AC1,同理可得到DB1=2DC1,易得![]() ;
;
(2)过B点作BE∥AC交AD的延长线于E点,根据平行线的性质和角平分线的定义得到∠E=∠CAD=∠BAD,则BE=AB,并且根据相似三角形的判定得△EBD∽△ACD,得到![]() ,而BE=AB,于是有
,而BE=AB,于是有![]() ,这实际是三角形的角平分线定理;
,这实际是三角形的角平分线定理;
(3)AD为△ABC的内角角平分线,由(2)的结论,根据相似三角形的判定得△DEF∽△ACF,利用相似三角形的性质解答即可.
解:(1)![]() 等边△ABC中,线段AD为其内角角平分线,
等边△ABC中,线段AD为其内角角平分线,
![]()
![]()
因为B1C1⊥AC于C1交AB的延长线于B1,
![]() ∠CAB=60°,∠B1=∠CAD=∠BAD=30°,
∠CAB=60°,∠B1=∠CAD=∠BAD=30°,
![]() AD=B1D,
AD=B1D,![]()
![]()
![]()
综上:这两个等式都成立;

(2)可以判断结论仍然成立,证明如下:
如图所示,△ABC为任意三角形,过B点作BE∥AC交AD的延长线于E点,
线段AD为其内角角平分线

![]() ∠E=∠CAD=∠BAD,△EBD∽△ACD
∠E=∠CAD=∠BAD,△EBD∽△ACD
∴BE=AB,![]()
又∵BE=AB.
∴![]() ,
,
即对任意三角形结论仍然成立;
(3)如图(2)所示,因为Rt△ABC中,∠ACB=90°,AC=8,![]() ,
,
![]()

∵AD为△ABC的内角角平分线,
∴
∵DE∥AC,
![]()
![]()
∵DE∥AC,
∴△DEF∽△ACF,![]()
∴![]()
![]()
![]()
![]()


科目:初中数学 来源: 题型:
【题目】为丰富学生课余生活,引领学生多读书、会读书、读好书,重庆一中聘请了西南师大教授讲授“诗歌赏析”.为激励学生积极参与,凡听课者每人发了一张带号码的入场券,授课结束后将进行抽奖活动.设立一等奖一名,获100元购书卡,二等奖3名分别获50元购书卡,三等奖6名分别获价值20元的书一本,纪念奖若干分别获价值2元的笔一支.工作人员对听课学生人数情况进行了统计,绘制了如下统计图:
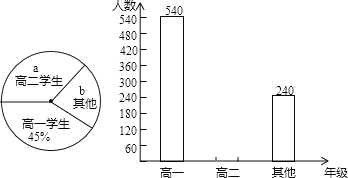
请根据以上信息解答下列问题
(1)这次授课共 名学生参加,扇形图中的a= ,b= ;
(2)补全条形统计图;
(3)学校共花费570元设奖,则本次活动中奖的概率是多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆心在坐标原点的⊙O,与坐标轴的交点分别为A、B和C、D.弦CM交OA于P,连结AM,已知tan∠PCO=![]() ,PC、PM是方程x2﹣px+20=0的两根.
,PC、PM是方程x2﹣px+20=0的两根.
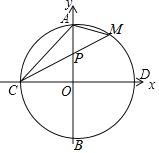
(1)求C点的坐标;
(2)写出直线CM的函数解析式;
(3)求△AMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
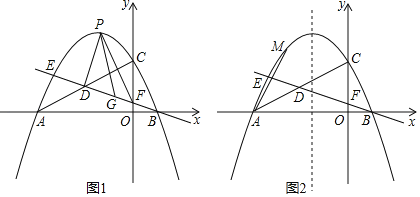
【题目】如图1,抛物线y=﹣![]() x2+bx+c的对称轴为直线x=﹣
x2+bx+c的对称轴为直线x=﹣![]() ,与x轴交于点A和点B(1,0),与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
,与x轴交于点A和点B(1,0),与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
(1)求抛物线的解析式;
(2)点P是直线BE上方抛物线上一动点,连接PD、PF,当△PDF的面积最大时,在线段BE上找一点G,使得PG﹣![]() EG的值最小,求出PG﹣
EG的值最小,求出PG﹣![]() EG的最小值.
EG的最小值.
(3)如图2,点M为抛物线上一点,点N在抛物线的对称轴上,点K为平面内一点,当以A、M、N、K为顶点的四边形是正方形时,请求出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爸爸沿街匀速行走,发现每隔7分钟从背后驶过一辆103路公交车,每隔5分钟从迎面驶来一辆103路公交车,假设每辆103路公交车行驶速度相同,而且103路公交车总站每隔固定时间发一辆车,那么103路公交车行驶速度是爸爸行走速度的__倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
.

(1)经过怎样的平移,可使△ABC的顶点A与坐标原点O重合,并直接写出此时点C 的对应点![]() 坐标;(不必画出平移后的三角形);
坐标;(不必画出平移后的三角形);
(2)将△ABC绕坐标原点![]() 逆时针旋转90°,得到△A′B′C′,画出△A′B′C′;
逆时针旋转90°,得到△A′B′C′,画出△A′B′C′;
(3)在(2)问的条件下,求线段BC扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com