
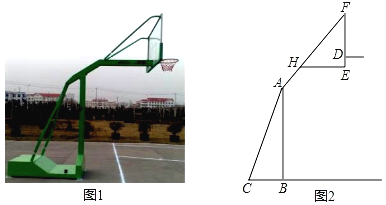
【题目】如图1、图2是某种品牌的篮球架实物图与示意图,已知底座BC=0.6米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.5米,篮板顶端F点到篮筐D的距离FD=1.4米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮筐D到地面的距离.(精确到0.1米,参考数据:cos75°≈0.3,sin75°≈0.9,tan75°≈3.7,![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
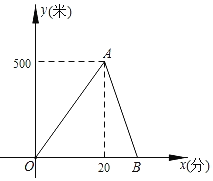
【题目】某湖边健身步道全长1500米,甲、乙两人同时从同一起点匀速向终点步行.甲先到达终点后立刻返回,在整个步行过程中,甲、乙两人间的距离y(米)与出发的时间x(分)之间的关系如图中OA﹣AB折线所示.
(1)用文字语言描述点A的实际意义;
(2)求甲、乙两人的速度及两人相遇时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连接AF,BF,EF,过点F作GF⊥AF交AD于点G,设![]() .
.
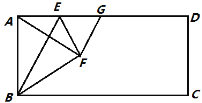
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC=![]() ,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
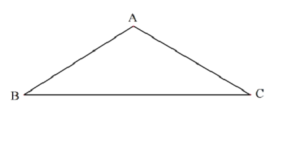
(1)求作圆O(尺规作图,保留作留痕迹,不写作法);
(2)求证:AC是OO的切线;
(3)若点P为圆O上一点,且弧PA=弧PB,连接PC,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠DAB=60°,AB=5,BC=3,点P从点D出发,沿DC,CB向终点B匀速运动.设点P所走过的路程为x,点P所经过的线段与AD,AP所围成的图形的面积为y,y随x的变化而变化.在下列图象中,能正确反映y与x的函数关系的是( )
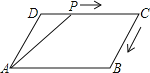
A.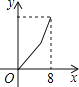 B.
B. C.
C.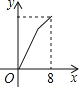 D.
D.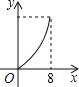
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列函数图象上任取不同两点P1(x1,y1)、P2(x2,y2),一定能使![]() <0成立的是( )
<0成立的是( )
A.y=3x﹣1(x<0)B.y=﹣x2+2x﹣1(x>0)
C.y=﹣![]() (x>0)D.y=x2﹣4x+1(x<0)
(x>0)D.y=x2﹣4x+1(x<0)
查看答案和解析>>
科目:初中数学 来源: 题型:
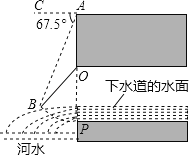
【题目】如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中OP为下水管道口直径,OB为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径OB=OP=100cm,OA为检修时阀门开启的位置,且OA=OB.
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达OB位置时,在点A处测得俯角∠CAB=67.5°,若此时点B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
(![]() =1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
=1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
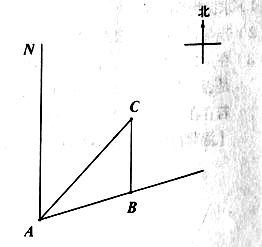
【题目】如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点![]() 处测得码头
处测得码头![]() 的船的东北方向,航行40分钟后到达
的船的东北方向,航行40分钟后到达![]() 处,这时码头
处,这时码头![]() 恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头
恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头![]() 的最近距离.(结果精确的0.1海里,参考数据
的最近距离.(结果精确的0.1海里,参考数据![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com