
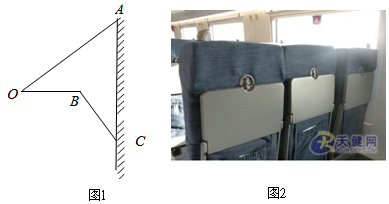
分析 延长CB交AO于点D.则CD⊥OA,在Rt△OBD中根据正弦函数求得BD,根据余弦函数求得OD,在Rt△ACD中,根据正切函数求得AD,然后根据AD+OD=OA=75,列出关于x的方程,解方程即可求得.
解答  解:延长CB交AO于点D.
解:延长CB交AO于点D.
∴CD⊥OA,
设BC=x,则OB=75-x,
在Rt△OBD中,OD=OB•cos∠AOB,BD=OB•sin∠AOB,
∴OD=(75-x)•cos37°=0.8(75-x)=60-0.8x,
BD=(75-x)sin37°=0.6(75-x)=45-0.6x,
在Rt△ACD中,AD=DC•tan∠ACB,
∴AD=(x+45-0.6x)tan37°=0.75(0.4x+45)=0.3x+33.75,
∵AD+OD=OA=75,
∴0.3x+33.75+60-0.8x=75,
解得x=37.5.
∴BC=37.5;
故小桌板桌面的宽度BC约为37.5cm.
点评 本题考查了解直角三角形的应用,解题的关键是正确构造直角三角形并求解.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
 某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.
某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 28×103 | B. | 2.8×104 | C. | 2.8×106 | D. | 0.28×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
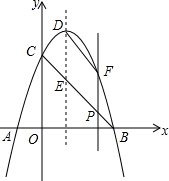 如图,抛物线y=-x2+2x+3与x轴交于点A、点B,与y轴交于点C,其顶点为D.线段BC与抛物线的对称轴交于点E.
如图,抛物线y=-x2+2x+3与x轴交于点A、点B,与y轴交于点C,其顶点为D.线段BC与抛物线的对称轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
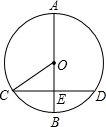 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com