
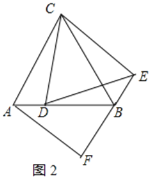
【题目】已知![]() 为等边三角形,点
为等边三角形,点![]() 是线段
是线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合).将线段
重合).将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() ,
,![]() .
.
(1)依题意补全图1并判断![]() 与
与![]() 的数量关系.
的数量关系.
(2)过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,用等式表示线段
,用等式表示线段![]() ,
,![]() 与
与![]() 之间的数量关系并证明.
之间的数量关系并证明.
【答案】(1)补全图形见解析,AD=BE;(2)![]() ,证明见解析
,证明见解析
【解析】
(1)根据题意补全图形,由等边三角形的性质得出AB=BC=AC,∠A=∠B=60°,由旋转的性质得:∠ACB=∠DCE=60°,CD=CE,得出∠ACD=∠BCE,证明△ACD≌△BCE,即可得出结论;
(2)由全等三角形的性质得出AD=BE,∠CBE=∠CAD=60°,求出∠ABF=180°-∠ABC-∠CBE=60°,在Rt△ABF中,由三角函数得出![]() ,
,![]() ,即可得出结论.
,即可得出结论.
(1)补全图形如图1所示,AD=BE,
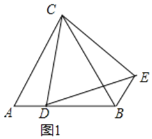
理由如下:
∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=60°,
由旋转的性质得:∠ACB=∠DCE=60°,CD=CE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
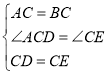 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)![]() ;理由如下:
;理由如下:
由(1)得:△ACD≌△BCE,
∴AD=BE,∠CBE=∠CAD=60°,
∴∠ABF=180°-∠ABC-∠CBE=60°,
∵AF⊥EB,
∴∠AFB=90°,
在Rt△ABF中,![]() ,
,
∴![]() ,
,
∵AD+DB=AB,
∴EB+DB=AB,
∴![]() .
.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,
,![]() 为反比例函数
为反比例函数![]() 上的两个动点,以
上的两个动点,以![]() ,
,![]() 为顶点构造菱形
为顶点构造菱形![]() .
.
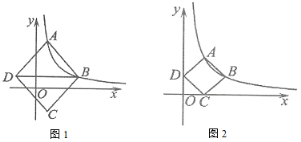
(1)如图1,点![]() ,
,![]() 横坐标分别为1,4,对角线
横坐标分别为1,4,对角线![]() 轴,菱形
轴,菱形![]() 面积为
面积为![]() .求
.求![]() 的值.
的值.
(2)如图2,当点![]() ,
,![]() 运动至某一时刻,点
运动至某一时刻,点![]() ,点
,点![]() 恰好落在
恰好落在![]() 轴和
轴和![]() 轴正半轴上,此时
轴正半轴上,此时![]() .求点
.求点![]() ,
,![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的变换点
的变换点![]() 的坐标定义如下:当
的坐标定义如下:当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ;当
;当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() 的变换点
的变换点![]() 的坐标是_________;点
的坐标是_________;点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() __________
__________![]() ;
;
(2)若点![]() 是函数
是函数![]() 图象上的一点,点
图象上的一点,点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,求线段
,求线段![]() 长的取值范围;
长的取值范围;
(3)已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() .点
.点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 的变换点为
的变换点为![]() .若点
.若点![]() 恰好在抛物线的对称轴上,且四边形
恰好在抛物线的对称轴上,且四边形![]() 是菱形,求
是菱形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
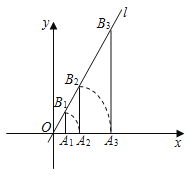
【题目】如图,点A1的坐标为(2,0),过点A1作x轴的垂线交过原点与x轴夹角为60°的直线l于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3按此做法进行下去,则点B2019的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
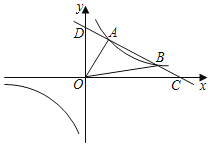
(1)求一次函数与反比例函数的解析式.
(2)求当x为何值时,y1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系,点 O 是原点,直线 y x 6分别交 x 轴,y 轴于点 B,A,经过点 A 的直线 y x b 交 x 轴于点 C.
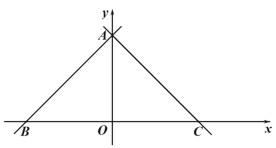
(1)求 b 的值 ;
(2)点 D 是线段 AB 上的一个动点,连接 OD,过点 O 作 OE⊥OD 交 AC 于点 E,连接DE,将△ODE 沿 DE 折叠得到△FDE,连接 AF.设点 D 的横坐标为 t,AF 的长为 d,当t> 3 时,求 d 与 t 之间的函数关系式(不要求写出自变量 t 的取值范围);
(3)在(2)的条件下,DE 交 OA 于点 G,且 tan∠AGD=3.点 H 在 x 轴上(点 H 在点O 的右侧),连接 DH,EH,FH,当∠DHF=∠EHF 时,请直接写出点 H 的坐标,不需要写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
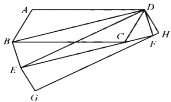
【题目】如图1,![]() ,
,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 均为平行四边形,且点
均为平行四边形,且点![]() 分别落在
分别落在![]() 上.
上.
(1)若![]() 的周长为16,用含
的周长为16,用含![]() 的代数式来表示
的代数式来表示![]() 的面积
的面积![]() ,并求出
,并求出![]() 的最大值;
的最大值;
(2)若四边形![]() 均为矩形,且
均为矩形,且![]() ,求
,求![]() 的值.
的值.
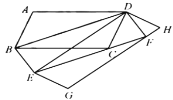
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com