
����Ŀ��ijУ��չ�����������������������ƹ���������ܲ��������������˶���Ŀ��ѧ��ֻ��ѡ������һ�֣�Ϊ�˽�ѧ��ϲ����һ����Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ����Ų�������ͳ��ͼ��������ͼ�е���Ϣ����������⣺
��1��������ϲ��������Ŀ�������ٷֱ��� ������������ͳ��ͼ�е�Բ�ĽǵĶ����� ��
��2��������ͳ��ͼ����������ע��������
��3����֪��У��1000��ѧ����������������ȫУϲ��ƹ����������Ƕ��٣�

���𰸡���1��20%��72�㣻��2���𰸼���������3��440��
�������������������1������1��ȥ����������ռ�ı����������ϲ������������ٷֱȣ����ðٷֱȳ���360�ȼ���������ε�Բ�ĽǵĶ�����
��2������ϲ��Aƹ�������44�ˣ�ռ44%������õ���������������Զ�Ӧ�İٷֱȼ������ϲ�����������������ͳ��ͼ��
��3��������1000����ϲ��ƹ�����������ռ�İٷֱȼ�����⣮
����������⣺��1��1��44%��8%��28%=20%����������ͳ��ͼ�е�Բ�ĽǵĶ����ǣ�360��20%=72�㣮�ʴ�Ϊ��20%��72�㣻
��2��������������ǣ�44��44%=100���ˣ�����ϲ������������ǣ�100��20%=20���ˣ���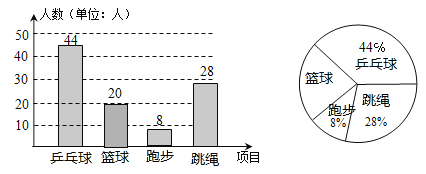 ��
��
��3��ȫУϲ��ƹ�����������1000��44%=440���ˣ���
�𣺸�����������ȫУϲ��ƹ�����������440�ˣ�


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����AB�Ķ���B��Ϧ�������������һ��б���ϵĵ�D����ijУ��ѧ������ȤС���ͬѧ���ڲ�����˵ĸ߶ȣ�����˵ĵײ�A����õ�D������Ϊ15�㣬AC=10�ף��ֲ����BDA=45�㣮��֪б��CD���¶�Ϊi=1��![]() �������AB�ĸ߶ȣ�
�������AB�ĸ߶ȣ�![]() ��1.7�������ȷ����λ����
��1.7�������ȷ����λ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У���֪A��2��2����B����2��0����C����1����2����

��1����ƽ��ֱ������ϵ�л�����ABC��
��2������D���C����y��Գƣ����D������Ϊ�� ����
��3�����ABC�������
��4����֪��PΪx����һ�㣬��S��ABP��5ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����Ӳ����ʩ�������ɹ�80̨���ԣ�����A��B�����ͺŵĵ��Կɹ�ѡ����֪ÿ̨A�͵��Ա�B�͵Ĺ�2000Ԫ��2̨A�͵�����3̨B�͵��Թ���24000Ԫ��
��1���ֱ���A��B�����ͺŵ��Եĵ��ۣ�
��2����A��B�����ͺŵ��ԵIJɹ��ܼ۲�����38��Ԫ����A�͵������ɹ�����̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У��ı���OABC�Ķ���A��x���ϣ���COA=��B=60������CB��OA��
��1����֤���ı���OABC��ƽ���ı��Σ�
��2����A������Ϊ��8��0����OC��Ϊ6�����B�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У�AC=6cm��BC=8cm��AB=10cm��CDΪAB���ϵĸߣ�����P�ӵ�A������������ABC����������ʱ����һȦ�ص�A�㣬�ٶ�Ϊ2cm/s�����˶�ʱ��Ϊt s��
��1����CD�ij���
��2��tΪ��ֵʱ����ACP�ǵ��������Σ�
��3����MΪBC��һ���㣬NΪAB��һ���㣬�Ƿ����M��Nʹ��AM+MN ��ֵ��С�������,��ֱ��д����Сֵ�����û�У���˵�����ɡ�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
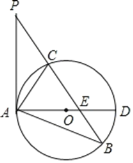
����Ŀ����ͼ����֪��![]() �У�C��BP����һ�㣬PA��
�У�C��BP����һ�㣬PA��![]() �����ߣ�
�����ߣ�![]() ��
��![]() �����Բ��AD��
�����Բ��AD��![]() ��ֱ�����ҽ�BP�ڵ�E��
��ֱ�����ҽ�BP�ڵ�E��
![]() ��֤��
��֤��![]() ��
��
![]() ����C��
����C��![]() ������Ϊ��F���ӳ�CF��AB�ڵ�G����
������Ϊ��F���ӳ�CF��AB�ڵ�G����![]() ��AF��
��AF��![]() ��3��
��3��![]()
����CF�ij���
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱���������ij��ҵ��������10̨��ˮ�����豸������A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ���������ķ����±���
A�� | B�� | |
�۸���Ԫ/̨�� | 12 | 10 |
������ˮ������/�£� | 240 | 200 |
�����ķѣ���Ԫ/̨�� | 1 | 1 |
��Ԥ�㣬����ҵ�����豸���ʽ���105��Ԫ��
��1�� ������Ƹ���ҵ�м��ֹ�����
��2��������ҵÿ�²�������ˮ��Ϊ2040�֣�Ϊ�˽�Լ�ʽ�Ӧѡ�����ֹ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com