
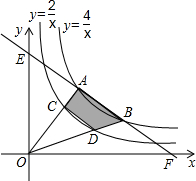
 已知,如图,双曲线y=
已知,如图,双曲线y=| 4 |
| x |
| 2 |
| x |
| 4 |
| x |
| 4 |
| m |
| 2 |
| m |
| OD |
| OB |
| 2 |
| 4 |
| 1 |
| 2 |
| OC |
| OA |
| OD |
| OB |
| OC |
| OA |
| OD |
| OB |
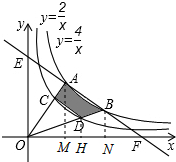 解:(1)如图,过点A作AM⊥x轴于点M,过点D作DH⊥x轴于点H,过点B作BN⊥x轴于点N,
解:(1)如图,过点A作AM⊥x轴于点M,过点D作DH⊥x轴于点H,过点B作BN⊥x轴于点N,| 4 |
| m |
| 2 |
| m |
| 1 |
| 2 |
| 2 |
| m |
| 4 |
| m |
| OD |
| OB |
| DH |
| BN |
| OH |
| ON |
| OD |
| OB |
| 2 |
| 4 |
| 1 |
| 2 |
| OC |
| OA |
| 1 |
| 2 |
| OC |
| OA |
| OD |
| OB |
| OC |
| OA |
| OD |
| OB |
| S△COD |
| S△AOB |
| OD |
| OB |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
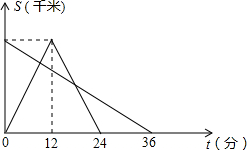 甲、乙两车同时分别从A、B两地出发相向而行,甲车到达B地后立即返回A地,若两车离A地的距离S(千米)与所用时间t(分)的函数关系如图,则甲、乙两车在途中两次相遇的间隔时间为
甲、乙两车同时分别从A、B两地出发相向而行,甲车到达B地后立即返回A地,若两车离A地的距离S(千米)与所用时间t(分)的函数关系如图,则甲、乙两车在途中两次相遇的间隔时间为查看答案和解析>>
科目:初中数学 来源: 题型:
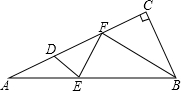 如图,在Rt△ABC中,∠CAB=30°,∠C=90°.AD=
如图,在Rt△ABC中,∠CAB=30°,∠C=90°.AD=| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com