
 已知矩形ABCD,AB=6,AD=4$\sqrt{3}$
已知矩形ABCD,AB=6,AD=4$\sqrt{3}$分析 (1)根据题意可知,要使得∠APB=90°,只要以AB为直径作圆,交于矩形内部的部分即是所求;
(2)根据题意作AB的垂直平分线,使得∠AOB=120°,然后再说明即可;
(3)要求DP得取值范围,只要找出DP的最大值和最小值即可,根据图2可知点P的轨迹是一条弧长,求出它的长度即可解答本题.
解答 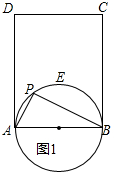 解:(1)如右图1所示,以AB为直径,$\widehat{AEB}$上除去端点A、B外的任何一点都符合要求,使得∠APB=90°,
解:(1)如右图1所示,以AB为直径,$\widehat{AEB}$上除去端点A、B外的任何一点都符合要求,使得∠APB=90°,
(2)如右图2所示,作AB的垂直平分线OE交AB与点F,使得∠AOB=120°,以OA长为半径作圆,交矩形ABCD于点M、N,则$\widehat{MEN}$上的任何一点都符合要求,使得∠APB=60°,则$\widehat{MEN}$为点P的轨迹;
(3)连接DO交⊙O于点P1,连接DM交⊙O于点P2(点N与点P2重合),如图2所示,
∵∠AOB=120°,
∴∠AOF=60°,∠OAF=30°,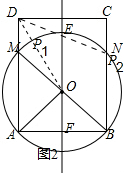
∵AB=6,AD=4$\sqrt{3}$,
∴AF=3,OF=AF•tan30°=$\sqrt{3}$,OA=$\sqrt{O{F}^{2}+A{F}^{2}}=\sqrt{(\sqrt{3})^{2}+{3}^{2}}=2\sqrt{3}$,
∴OD=$\sqrt{{3}^{2}+(4\sqrt{3}-\sqrt{3})^{2}}=6$,
∴DP1=6-2$\sqrt{3}$,
∵OF=$\sqrt{3}$,BC=4$\sqrt{3}$,
∴CP2=4$\sqrt{3}-\sqrt{3}-\sqrt{3}$=2$\sqrt{3}$,
∵CD=6,
∴DP2=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$,
即DP的取值范围是($6-2\sqrt{3}$,4$\sqrt{3}$),
点P的轨迹长为$\widehat{MEN}$的长,
∵$\widehat{MEN}$=$\frac{120π×2\sqrt{3}}{180}$=$\frac{4\sqrt{3}π}{3}$,
∴点P的轨迹的长为$\frac{4\sqrt{3}π}{3}$.
点评 本题考查四边形综合题,解题的关键是明确题意,找出所求问题需要的条件,根据题目中的条件可以画出相应的图形,利用数形结合的思想解答问题.


科目:初中数学 来源: 题型:选择题
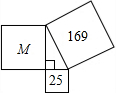 如图,喜羊羊和美羊羊分别做了面积为25和169的两个正方形纸板,村长看到后,把他俩做的正方形和沸羊羊做的正方形M如图放在一起,中间空出的三角形正好是直角三角形,那么正方形M的面积是( )
如图,喜羊羊和美羊羊分别做了面积为25和169的两个正方形纸板,村长看到后,把他俩做的正方形和沸羊羊做的正方形M如图放在一起,中间空出的三角形正好是直角三角形,那么正方形M的面积是( )| A. | 12 | B. | 13 | C. | 144 | D. | 194 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,要拧开一个边长是2的正六边形螺母,扳手张开的开口a的取值为( )
如图,要拧开一个边长是2的正六边形螺母,扳手张开的开口a的取值为( )| A. | 2$\sqrt{3}$≤a≤4 | B. | a≤4 | C. | $\sqrt{3}$≤a≤2 | D. | a≥2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com