
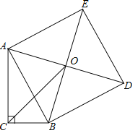
【题目】在直角三角形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,连接
,连接![]() 、
、![]() 交
交![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
延长CB,过点D作CB延长线的垂线,交点为F,过点O作OM⊥CF,先证明RT△ACB≌RT△BFD,然后分别表示出OM、CM的长度,在RT△OCM中利用勾股定理可得出答案.
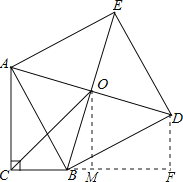
延长CB过点D作CB延长线的垂线,交点为F,过点O作OM⊥CF,
则可得OM是梯形ACFD的中位线,
∵∠ABC+∠FBD=∠CAB+∠ABC=90°,
∴∠CAB=∠FBD,
在RT△ACB和RT△BFD中,
∵AB=BD,∠CAB=∠FBD,∠ACB=∠BFD,
∴RT△ACB≌RT△BFD,
∴AC=BF,BC=DF,
设AC=x,则OM=![]() ,CM=
,CM=![]() ,
,
在RT△OCM中,OM2+CM2=OC2,即2(![]() )2=18,
)2=18,
解得:x=4,即AC的长度为4.
故选C.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】某民俗旅游村为接待游客住宿需要,开设了有![]() 张床位的旅馆,当每张床位每天收费
张床位的旅馆,当每张床位每天收费![]() 元时,床位可全部租出.若每张床位每天收费提高
元时,床位可全部租出.若每张床位每天收费提高![]() 元,则相应的减少了
元,则相应的减少了![]() 张床位租出.如果每张床位每天以
张床位租出.如果每张床位每天以![]() 元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 14元 B. 15元 C. 16元 D. 18元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生每天参加户外活动的情况,随机抽查了100名学生每天参加户外活动的时间情况,并将抽查结果绘制成如图所示的扇形统计图.
请你根据图中提供的信息解答下列问题:

(1)请直接写出图中![]() 的值,并求出本次抽查中学生每天参加户外活动时间的中位数;
的值,并求出本次抽查中学生每天参加户外活动时间的中位数;
(2)求本次抽查中学生每天参加户外活动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,我们可以利用
,我们可以利用![]() 与
与![]() 相似证明
相似证明![]() ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;
(结论运用)如图![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是对角线
是对角线![]() 、
、![]() 的交点,点
的交点,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
(1)试利用射影定理证明![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
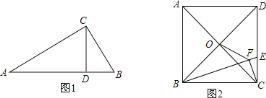
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
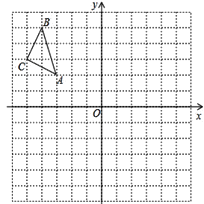
【题目】如图,已知:在平面直角坐标系中,每个小正方形的边长为1,△ABC的顶点都在格点上,点A的坐标为(-3,2).请按要求分别完成下列各小题:
(1)把△ABC向下平移7个单位,再向右平移7个单位,得到△A1B1C1,画出△A1B1C1;
(2)画出△A1B1C1关于x轴对称的△A2B2C2;
画出△A1B1C1关于y轴对称的△A3B3C3;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古代名著《算学启蒙》中有一题:“良马日行二百四十里.驽马日行一百五十里.驽马先行十二日,问良马几日追及之”,如图是两马行走的路程![]() 关于时间
关于时间![]() 的函数图像.
的函数图像.
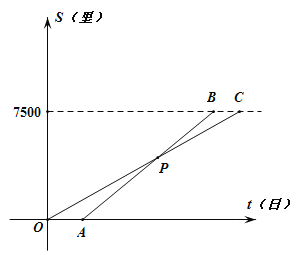
(1)![]() 的函数解析式为_______.
的函数解析式为_______.
(2)求![]() 点的坐标.
点的坐标.
(3)若两匹马先在甲站,再从甲站出发行往乙站,并停留在乙站,且甲、乙两站之间的路程为![]() 里,请问
里,请问![]() 为何值时,驽马与良马相距
为何值时,驽马与良马相距![]() 里?
里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com