Question

【题目】在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E，DF与线段AC（或AC的延长线）相交于点F．

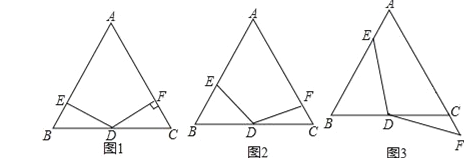
（1）如图1，若DF⊥AC，垂足为F，AB=4，求BE的长；

（2）如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F．求证：BE+CF=AB．

（3）如图3，若∠EDF的两边分别交AB、AC的延长线于E、F两点，（2）中的结论还成立吗？如果成立，请证明；如果不成立，请直接写出线段BE、AB、CF之间的数量关系．

Answer 1

【答案】（1）1（2）证明见解析（3）结论不成立．结论：BE﹣CF=AB

【解析】

试题分析：（1）如图1中，只要证明∠BED=90°，根据直角三角形30度角性质即可解决问题．

（2）如图2中，过点D作DM⊥AB于M，作DN⊥AC于N．只要证明△BDM≌△CDN，△EDM≌△FDN即可解决问题．

（3）（2）中的结论不成立．结论：BE﹣CF=AB，证明方法类似（2）．

试题解析：（1）如图1中，

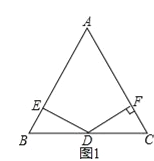
∵AB=AC，∠A=60°，

∴△ABC是等边三角形，

∴∠B=∠C=60°，BC=AC=AB=4，

∵点D是线段BC的中点，

∴BD=DC=BC=2，

∵DF⊥AC，即∠CFD=90°，

∴∠CDF=30°，

又∵∠EDF=120°，

∴∠EDB=30°，

∴∠BED=90°

∴BE=BD=1．

（2）如图2中，过点D作DM⊥AB于M，作DN⊥AC于N．

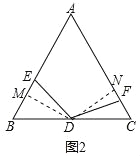
∵∠B=∠C=60°，BD=DC，∠BDM=∠CDN=30°，

∴△BDM≌△CDN，

∴BM=CN，DM=DN，

又∵∠EDF=120°=∠MDN，

∴∠EDM=∠NDF，

又∵∠EMD=∠FND=90°，

∴△EDM≌△FDN，

∴ME=NF，

∴BE+CF=BM+EM+NC﹣FN=2BM=BD=AB．

（3）结论不成立．结论：BE﹣CF=AB．

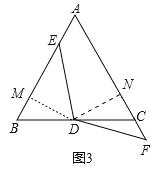
∵∠B=∠C=60°，BD=DC，∠BDM=∠CDN=30°，

∴△BDM≌△CDN，

∴BM=CN，DM=DN，

又∵∠EDF=120°=∠MDN，

∴∠EDM=∠NDF，

又∵∠EMD=∠FND=90°，

∴△EDM≌△FDN，

∴ME=NF，

∴BE﹣CF=BM+EM﹣（FN﹣CN）=2BM=BD=AB．