
 如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )
如图,点P是正方形ABCD内一点,将△ABP绕着B沿顺时针方向旋转到与△CBP′重合,若PB=3,则PP′的长为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 3 | D. | 无法确定 |
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
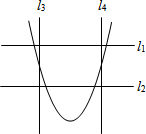 如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )| A. | l1为x轴,l3为y轴 | B. | l1为x轴,l4为y轴 | C. | l2为x轴,l3为y轴 | D. | l2为x轴,l4为y轴 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
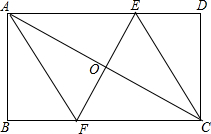 如图,已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O,连接AF、CE.
如图,已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O,连接AF、CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
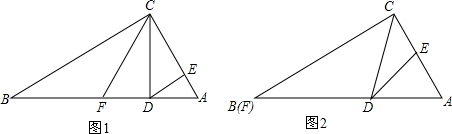
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
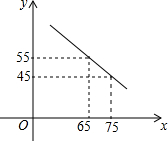 某商场以每件60元的进价购进乙种T恤衫,在销售中发现这种T恤衫的销售数量y(件)与销售价格x(元)满足一次函数,其图象如图所示,同时物价部门规定售价不得低于进价且获利不得高于进价的45%.
某商场以每件60元的进价购进乙种T恤衫,在销售中发现这种T恤衫的销售数量y(件)与销售价格x(元)满足一次函数,其图象如图所示,同时物价部门规定售价不得低于进价且获利不得高于进价的45%.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
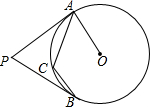 如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )
如图,PA,PB分别与⊙O相切于A、B,点C在劣弧AB上(不与A,B重合),若∠APB=70°,则∠ACB=( )| A. | 140° | B. | 145° | C. | 110° | D. | 125° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
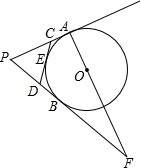 如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D,连接AO并延长交PB的延长线于点F.若⊙O的半径为r,△PCD的周长等于3r,则$\frac{OA}{OF}$的值是$\frac{5}{13}$.
如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB于点C,D,连接AO并延长交PB的延长线于点F.若⊙O的半径为r,△PCD的周长等于3r,则$\frac{OA}{OF}$的值是$\frac{5}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
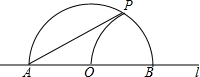 如图,直线l上一点O,以O为圆心,任意长为半径画半圆,交l于A、B两点,再以B为圆心,OB的长为半径画弧交半圆于P,连AP,则sin∠PAB的值等于$\frac{1}{2}$.
如图,直线l上一点O,以O为圆心,任意长为半径画半圆,交l于A、B两点,再以B为圆心,OB的长为半径画弧交半圆于P,连AP,则sin∠PAB的值等于$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com