
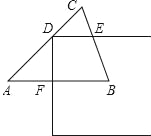
【题目】如图,在△ABG中,AB=AC=1,∠A=45°,边长为1的正方形的一个顶点D在边AG上,与△ADC另两边分别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重含),设AF=x,正方形与△ABC重叠部分的面积为y.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)x为何值时y的值最大?
【答案】(1)![]() (
(![]() ) (2)
) (2)![]()
【解析】
(1)当点D保持在AC上时,正方形与△ABC重叠部分为直角梯形DEBF,根据直角梯形的面积公式,只需用含x的代数式分别表示出上底DE、下底BF及高DF的长度即可.由△ADF为等腰直角三角形,可得高DF=AF=x;则AD=![]() x,下底BF=AB-AF=1-x;进而得出CD=AC-AD=1-
x,下底BF=AB-AF=1-x;进而得出CD=AC-AD=1-![]() x,再根据等腰三角形及平行线的性质可证∠C=∠CED,得出上底DE=CD=1-
x,再根据等腰三角形及平行线的性质可证∠C=∠CED,得出上底DE=CD=1-![]() x;根据点D保持在AC上,且D不与A重合,可知0<AD≤1,从而求出自变量x的取值范围;
x;根据点D保持在AC上,且D不与A重合,可知0<AD≤1,从而求出自变量x的取值范围;
(2)由(1)知,y是x的二次函数,根据二次函数的性质,可知当x=-![]() 时,y的值最大;
时,y的值最大;
解:(1)∵AB=AC,
∴∠B=∠C,
∵DE∥AB,
∴∠B=∠CED,∠AFD=∠FDE=90°,
∴∠C=∠CED,
∴DC=DE.
在Rt△ADF中,∵∠A=45°,
∴∠ADF=45°=∠A,
∴AF=DF=x,
∴AD=![]() ,
,
∴DC=DE=1﹣![]() x,
x,
∴y=![]() (DE+FB)×DF=
(DE+FB)×DF=![]() (1﹣
(1﹣![]() x+1﹣x)x=﹣
x+1﹣x)x=﹣![]() (
(![]() +1)x2+x.
+1)x2+x.
∵点D保持在AC上,且D不与A重合,
∴0<AD≤1,
∴0<![]() x≤1,
x≤1,
∴0<x≤![]() .
.
故y=﹣![]() (
(![]() +1)x2+x,自变量x的取值范围是0<x≤
+1)x2+x,自变量x的取值范围是0<x≤![]() ;
;
(2)∵y=﹣![]() (
(![]() +1)x2+x,
+1)x2+x,
∴当x=-![]() =
=![]() ﹣1时,y有最大值.
﹣1时,y有最大值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
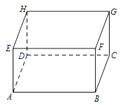
【题目】如图 所示,一个长方体的长、宽、高分别是 ![]() ,
,![]() ,
,![]() ,有一只蚂蚁从点
,有一只蚂蚁从点 ![]() 出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点
出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点 ![]() 时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
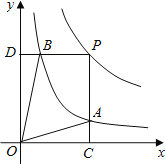
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+px+q的对称轴为直线x=﹣2,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(﹣1,﹣1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( ).

A. (0,﹣2) B. (0,﹣![]() ) C. (0,﹣
) C. (0,﹣![]() ) D. (0,﹣
) D. (0,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自贡是“盐之都,龙之乡,灯之城”,文化底蕴深厚.为弘扬乡土特色文化,某校就同学们对“自贡历史文化”的了解程度进行随机抽样调查,将调查结果绘制成如下两幅统计图:
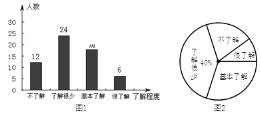
⑴本次共调查 名学生,条形统计图中![]() = ;
= ;
⑵若该校共有学生1200名,则该校约有 名学生不了解“自贡历史文化”;
⑶调查结果中,该校九年级(2)班学生中了解程度为“很了解”的同学进行测试,发现其中共有四名同学相当优秀,它们是三名男生,一名女生,现准备从这四名同学中随机抽取两人去市里参加“自贡历史文化”知识竞赛,用树状图或列表法,求恰好抽取一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某购物中心试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价且获利不得高于 50%.经试销发现,销售量y(件)与销售单价x(元)的关系符合一次函数yx140.
(1)若销售该服装获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价为多少元时,可获得最大利润?最大利润是多少元?
(2)当获得利润为1200元时,求销售单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1.有下列结论:①b2=4ac ②abc>0 ③a>c ④4a+c>2b.其中结论正确的个数是( )
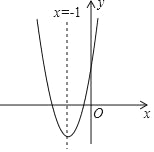
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
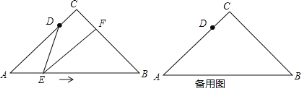
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一点,且AD=3cm,动点
边上一点,且AD=3cm,动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 向终点
向终点![]() 运动.作
运动.作![]() ,与边
,与边![]() 相交于点
相交于点![]() .
.
![]() 找出图中的一对相似三角形,并说明理由;
找出图中的一对相似三角形,并说明理由;
![]() 当
当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长;
的长;
![]() 求动点
求动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 向终点
向终点![]() 运动的过程中点
运动的过程中点![]() 的运动路线长.
的运动路线长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com