练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，△ABC绕点C顺时针旋转得△A1B1C，当A1落在AB边上时，连接B1B，取BB1的中点D，连接A1D，则A1D的长度是 ．

    【答案】
    【解析】∵∠ACB=90°，∠ABC=30°，AC=2，

    ∴∠A=90°﹣∠ABC=60°，AB=4，BC=2 ，

    ∵CA=CA1，

    ∴△ACA1是等边三角形，AA1=AC=BA1=2，

    ∴∠BCB1=∠ACA1=60°，

    ∵CB=CB1，

    ∴△BCB1是等边三角形，

    ∴BB1=2 ，BA1=2，∠A1BB1=90°，

    ∴BD=DB1= ，

    ∴A1D= = ，

    故答案为： ．

    由旋转的性质及等边三角形的性质可得△BCB1是等边三角形，∠A1BB1=90°，利用勾股定理可求出A1D长.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算题:计算
    （1）计算：（ ）﹣1﹣3tan30°+（1﹣π）0 ．
    （2）解分式方程： = ﹣1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年秋季，长白山土特产喜获丰收，某土特产公司组织10辆汽车装运甲、乙、丙三种土特产去外地销售，按计划10辆车都要装运，每辆汽车只能装运同一种土特产，且必须装满．设装运甲种土特产的汽车有x辆，装运乙种土特产的汽车有y辆，根据下表提供的信息，解答以下问题．

    （1）装运丙种土特产的车辆数为（用含x、y的式子表示）；

    （2）用含x、y的式子表示这10辆汽车共装运土特产的吨数；

    （3）求销售完装运的这批土特产后所获得的总利润（用含x、y的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是边长为4cm的等边三角形，动点P从点A出发，以2cm/s的速度沿A→C→B运动，到达B点即停止运动，过点P作PD⊥AB于点D，设运动时间为x（s），△ADP的面积为y（cm2），则能够反映y与x之间函数关系的图象大致是（ ）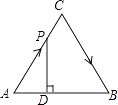

    A.
    B.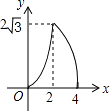
    C.
    D.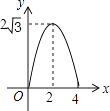

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知O为直线BC上一定点，点A在直线外一定点．在直线BC上取点P，使得以O、A、P为顶点的三角形为等腰三角形．

    (1)当∠AOC=30°时，如果我们通过分类讨论、画图尝试可以找到满足条件的点P共有______个．

    (2)若在直线BC上有且只有两个满足条件的点P，则∠AOC=______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点 O 在直线 AB 上，OC⊥OD，∠EDO 与∠1 互余．

    (1)求证：ED//AB；

    (2)OF 平分∠COD 交 DE 于点 F，若OFD=70，补全图形，并求∠1 的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践：

    如图1，已知△ABC为等边三角形，点D，E分别在边AB、AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点．

    （1）观察猜想：在图1中，线段PM与PN的数量关系是　 　，∠MPN的度数是　 　；

    （2）探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，

    ①判断△PMN的形状，并说明理由；

    ②求∠MPN的度数；

    （3）拓展延伸：若△ABC为直角三角形，∠BAC=90°，AB=AC=10，点DE分别在边AB，AC上，AD=AE=4，连接DC，点M，P，N分别为DE，DC，BC的中点．把△ADE绕点A在平面内自由旋转，如图3，请直接写出△PMN面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=5，AC=3，AD，AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB于点F，连结DH，则线段DH的长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在电线杆上的C处引拉线CE、CF固定电线杆，拉线CE和地面成60°角，在离电线杆6米的B处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长（结果保留根号）．

    查看答案和解析>>

    同步练习册答案