
| A. | 互相垂直 | B. | 平行 | ||
| C. | 相交但不垂直 | D. | 平行或相交都有可能 |
分析 利用平行线的性质:两直线平行,同位角相等.那么同位角的平分线所分得的角也相等,再根据同位角相等,两直线平行的判定就可证明.
解答 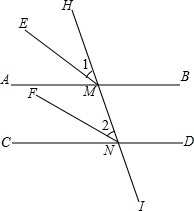 解:如图,AB∥CD,HI与AB,CD分别交于点M、N,EM,FN分别是∠AMH,∠CNH的平分线,
解:如图,AB∥CD,HI与AB,CD分别交于点M、N,EM,FN分别是∠AMH,∠CNH的平分线,
∵AB∥CD,
∴∠AMH=∠CNH(两直线平行,同位角相等),
∵EM,FN分别是∠AMH,∠CNH的平分线,
∴∠1=∠2,
∴EM∥FN(同位角相等,两直线平行),
∴∠1=$\frac{1}{2}$∠AMH,∠2=$\frac{1}{2}$∠CNH,
∴∠1=∠2,
∴EM∥FN(同位角相等,两直线平行).
故选:B.
点评 此题考查了平行线的判定与角平分线的定义.注意文字题的求解方法:首先根据题意画图,用数学语言表示出已知求证,再证明.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
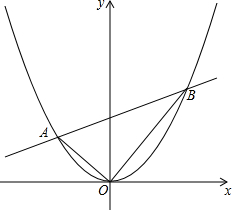 已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)
已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
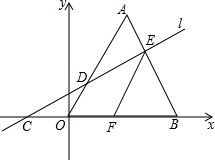 如图,在平面直角坐标系中,△A0B是边长为3的等边三角形,直线l与x轴、0A、AB分别交于点C、D、E,0C=AE.过点E作EF∥0A,交x轴于点F.
如图,在平面直角坐标系中,△A0B是边长为3的等边三角形,直线l与x轴、0A、AB分别交于点C、D、E,0C=AE.过点E作EF∥0A,交x轴于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
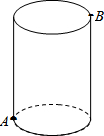 如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)
如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com