
| A | B | C | |
| 甲 | 10 | 5 | 6 |
| 乙 | 4 | 8 | 15 |
分析 根据题中表格信息,可以先设乙基地向A提供xt,向B提供yt,根据关系可以得甲、乙两个蔬菜基地,分别向A、B、C三个农贸市场提供同品种蔬菜的吨数,然后列出式子,根据x和y的取值范围得出答案.
解答 解:设甲蔬菜基地分别向A、B两个农贸市场提供蔬菜x、y吨,则调运量如下表,总运费为w(元),
| A | B | C | |
| 甲(单位:吨) | x | y | 60-x-y |
| 乙(单位:吨) | 45-x | 75-y | x+y-20 |
| A | B | C | |
| 甲(单位:吨) | 0 | 20 | 40 |
| 乙(单位:吨) | 45 | 55 | 0 |
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | “打开电视,正在播放《新闻联播》”是必然事件 | |
| B. | 在两个等圆中,相等的圆心角所对的弧相等,所对的弦也相等 | |
| C. | 数据1,1,2,2,3的中位数为2,极差为2,众数也为2 | |
| D. | 一组数据的方差越小,这组数据波动越大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
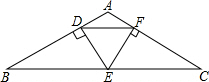 如图,△DEF是等边三角形,BC过点E,且平行于DF,又AB⊥ED,AC⊥EF,D,F是垂足.
如图,△DEF是等边三角形,BC过点E,且平行于DF,又AB⊥ED,AC⊥EF,D,F是垂足.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com