
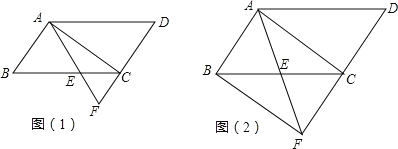
【题目】如图,在平行四边形ABCD中,AB≠BC,连接AC,AE是∠BAD的平分线,交边DC的延长线于点F.
(1)证明:CE=CF;
(2)如图(2),连接BF,若∠ABC=60°,BC=2AB,试判断四边形ABFC的形状,并说明理由.
【答案】(1)见解析(2)矩形,理由见解析
【解析】
(1)利用角平分线的性质结合平行四边形的性质得出∠BAF=∠F,∠DAF=∠CEF,进而得出答案;
(2)利用等边三角形的判定方法得出△ABE是等边三角形,进而得出△ABE≌△FCE(ASA),即可得出AB=FC,进而结合矩形的判定方法求出即可.
(1)∵AE是∠BAD的平分线,
∴∠BAF=∠DAF,
∵在平行四边形ABCD中,
∴AB∥DF,AD∥BC,
∴∠BAF=∠F,∠DAF=∠CEF,
∴∠F=∠DAF=∠CEF,
∴CE=FC;
(2)解:四边形ABFC是矩形,
理由:如图(2),∵∠ABC=60°,AD∥BC,
∴∠BAD=120°,
∵∠BAF=∠DAF,
∴∠BAF=60°,
则△ABE是等边三角形,
可得AB=BE=AE,∠BEA=∠AFC=60°,
∵BC=2AB,
∴AE=BE=EC,
∴△ABC是直角三角形,∠BAC=90°,
在△ABE和△FCE中
∵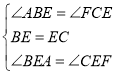 ,
,
∴△ABE≌△FCE(ASA),
∴AB=FC,
又∵AB∥FC,
∴四边形ABFC是平行四边形,
再由∠BAC=90°,
故四边形ABFC是矩形.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图所示,![]() 是
是![]() 外一点,
外一点,![]() ,
,![]() 分别和
分别和![]() 切于
切于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 上任意一点,过
上任意一点,过![]() 作
作![]() 的切线分别交
的切线分别交![]() ,
,![]() 于
于![]() ,
,![]() .
.

![]() 若
若![]() 的周长为
的周长为![]() ,则
,则![]() 的长为________;
的长为________;
![]() 连接
连接![]() 、
、![]() ,若
,若![]() ,则
,则![]() 的度数为________度.
的度数为________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,直线
,直线![]() 过点
过点![]() .
.
(1)当![]() 时,如图1,分别过点
时,如图1,分别过点![]() 和
和![]() 作
作![]() 直线
直线![]() 于点
于点![]()
![]() 直线
直线![]() 于点
于点![]() 与
与![]() 是否全等,并说明理由;
是否全等,并说明理由;
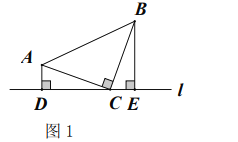
(2)当![]() 时,如图2,点
时,如图2,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() 点
点![]() 在
在![]() 上,点
上,点![]() 是
是![]() 上一点,分别过点
上一点,分别过点![]() 作
作![]() 直线
直线![]() 于点
于点![]() 直线
直线![]() 于点
于点![]() ,点
,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿
的速度沿![]() 路径运动,终点为
路径运动,终点为![]() 点
点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿
的速度沿![]() 路径运动,终点为
路径运动,终点为![]() ,点
,点![]() 同时开始运动,各自达到相应的终点时停止运动,设运动时间为
同时开始运动,各自达到相应的终点时停止运动,设运动时间为![]() 秒.
秒.

①当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]() 的值;
的值;
②当![]() 与
与![]() 全等时,求
全等时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
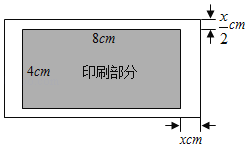
【题目】如图,印刷一张矩形的包装纸,印刷部分的长为8cm,宽为4cm,上下空白宽各![]() cm,左右空白宽各xcm,四周空白处的面积为Scm2.
cm,左右空白宽各xcm,四周空白处的面积为Scm2.
(1)求S与x的关系式;
(2)当四周空白处的面积为18cm2时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠B=90°,AB=9,BC=12,点p从点A开始延边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P.Q分别从A.B同时出发,当点Q运动到点C时,两点停止运动,问:
(1)填空:BQ=______,PB=______(用含t的代数式表示)
(2)经过几秒,PQ的长为 ![]() cm?
cm?
(3)经过几秒,![]() 的面积等于
的面积等于![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若三个非零实数x、y、z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x、y、z构成“和谐三数组”.
(1)实数1、2、3可以构成“和谐三数组”吗?请说明理由;
(2)若![]() 三点均在
三点均在![]() (k为常数,k≠0)的图像上,且这三点的纵坐标
(k为常数,k≠0)的图像上,且这三点的纵坐标![]() 构成“和谐三数组”,求实数t的值.
构成“和谐三数组”,求实数t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com