
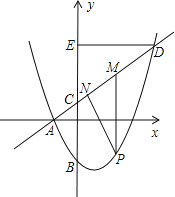
【题目】如图,抛物线![]() 与x轴交于点A(-2,0),交y轴于点B(0,
与x轴交于点A(-2,0),交y轴于点B(0,![]() ).直线
).直线![]() 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.
(1) 求抛物线![]() 与直线
与直线![]() 的解析式;
的解析式;
(2)点P是抛物线上A、D间的一个动点,过P点作PM∥CE交线段AD于M点.
①过D点作DE⊥y轴于点E,问是否存在P点使得四边形PMEC为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
②作PN⊥AD于点N,设△PMN的周长为m,点P的横坐标为x,求m关于x的函数关系式,并求出m的最大值.
【答案】(1)![]() ,
,![]() ;(2)① 存在,点P的坐标是(2,-3)和(4,
;(2)① 存在,点P的坐标是(2,-3)和(4,![]() );②
);②![]() , m的最大值是15.
, m的最大值是15.
【解析】
(1)将点A和点B的坐标代入抛物线的解析式可求得b、c的值,然后可求得抛物线的解析式,将点A的坐标代入直线的解析式可求得k的值,从而可求得直线的解析式;
(2)①将![]() 与
与![]() 联立,可求得点
联立,可求得点![]() ,然后再求得点
,然后再求得点![]() 则
则![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,则
,则![]() 的坐标是
的坐标是![]() .然后可得到
.然后可得到![]() 的长与
的长与![]() 的函数关系式,然后依据
的函数关系式,然后依据![]() ,可求得
,可求得![]() 的值,从而可得到点
的值,从而可得到点![]() 的坐标;
的坐标;
②在![]() 中,依据勾股定理可知:
中,依据勾股定理可知:![]() ,则
,则![]() 的周长是24,接下来,证明
的周长是24,接下来,证明![]() ,依据相似三角形的周长比等于相似比可得到
,依据相似三角形的周长比等于相似比可得到![]() 与x的函数关系式,最后利用配方法可求得
与x的函数关系式,最后利用配方法可求得![]() 的最大值.
的最大值.
解:(1)![]() 经过点
经过点![]() 和点
和点![]() ,
,
![]()
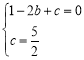 ,
,
解得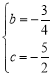 ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ,
,
![]() 直线
直线![]() 经过点
经过点![]() ,
,
![]() ,解得:
,解得:![]() .
.
![]() 直线的解析式为
直线的解析式为![]() ;
;
(2)①将![]() 与
与![]() 联立,解得
联立,解得![]() 或
或![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
![]() ,
,
![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() 的坐标是
的坐标是![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 的下方,
的下方,
![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,
![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 当点
当点![]() 的坐标为
的坐标为![]() 或
或![]() 时,四边形
时,四边形![]() 为平行四边形;
为平行四边形;
②在![]() 中,
中,![]() ,
,![]() ,
,
依据勾股定理可知:![]() ,
,
![]() 的周长是24,
的周长是24,
![]() 轴,
轴,
![]() ,
,
又![]() ,
,
![]() ,
,
![]()
![]() ,即
,即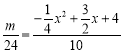 ,
,
化简整理得:![]() ,
,
配方得:![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最大值,
有最大值,![]() 的最大是15.
的最大是15.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2015秒时,点P的坐标是( ).
个单位长度,则第2015秒时,点P的坐标是( ).
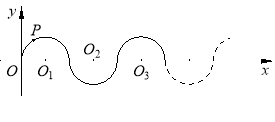
A.(2014,0) B.(2015,-1) C. (2015,1) D. (2016,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将
将![]() 折叠,得
折叠,得![]() .
.
(1)如图所示,当![]() 时,
时,![]() _______度;
_______度;

(2)如图所示,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 为
为![]() 中点时,点
中点时,点![]() 是边
是边![]() 上不与点
上不与点![]() 、
、![]() 重合的一个动点,将
重合的一个动点,将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() ,连接
,连接![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计.
成绩x(分) | 频数 | 频率 |
50≤x<60 | 10 | a |
60≤x<70 | 16 | 0.08 |
70≤x<80 | b | 0.20 |
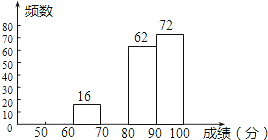
请你根据以上的信息,回答下列问题:
(1) a= ,b= ;
(2) 在扇形统计图中,“成绩x满足50≤x<60”对应扇形的圆心角大小是 ;
(3) 若将得分转化为等级,规定:50≤x<60评为D,60≤x<70评为C,70≤x<90评为B,90≤x<100评为A.这次全区八年级参加竞赛的学生约有 学生参赛成绩被评为“B”?
查看答案和解析>>
科目:初中数学 来源: 题型:
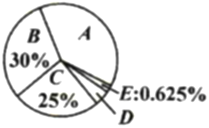
【题目】十九大召开后,某社区开展了“市民对十九大的关注情况”调查,采用随机抽样的方法访问了部分年龄在18周岁以上的城乡居民.小聪根据调查数据绘制了如下不完整的频数分布置表和扇形统计图.请根据图表解答下列问题.
关注情况 | 频数 |
非常关注( | 128 |
比较关注( | |
一般关注( | 80 |
不太关注( | |
不关注( | 2 |
(1)请完成频数分布表空格数据填写;
(2)求“非常关注”部分扇形圆心角的度数;
(3)若该社区18周岁以上居民共有20000人,请估计“比较关注”和“非常关注”的居民共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
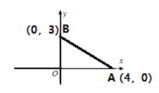
【题目】如图,已知点A的坐标为(4,0),点B的坐标为(0,3),在第一象限内找一点P(a,b) ,使△PAB为等边三角形,则2(a-b)=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根![]() .
.
(1)求实数k的取值范围.
(2)若方程两实根![]() 满足|x1|+|x2|=x1·x2,求k的值.
满足|x1|+|x2|=x1·x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
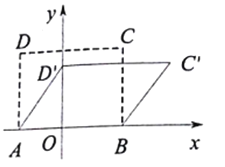
【题目】四边形具有不稳定性,如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 在
在![]() 轴上,且点
轴上,且点![]() ,边
,边![]() 长为
长为![]() .现固定边
.现固定边![]() ,向右推动矩形使点
,向右推动矩形使点![]() 落在
落在![]() 轴上(落点记为
轴上(落点记为![]() ),点
),点![]() 的对应点记为
的对应点记为![]() ,已知矩形
,已知矩形![]() 与推动后形成的平行四边形
与推动后形成的平行四边形![]() 的面积比为
的面积比为![]() ,则点
,则点![]() 坐标为_______.
坐标为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com