
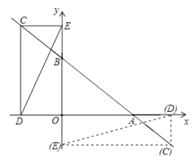
【题目】在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B,
(1)k的值是 ;
(2)点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.
①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求OCED的周长;
②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为![]() ,请直接写出点C的坐标.
,请直接写出点C的坐标.

【答案】(1)![]() ;(2)①8+4
;(2)①8+4![]() ;②点C的坐标为(﹣3,
;②点C的坐标为(﹣3,![]() )或(11,
)或(11,![]() ).
).
【解析】
(1)根据点A的坐标,利用待定系数法可求出k值;
(2)①利用一次函数图像上点的坐标特征可得出点B的坐标,由平行四边形的性质结合点E为OB的中点可得出CE是△ABO的中位线,结合点A的坐标可得出CE的长,在Rt△DOE中,利用勾股定理可求出DE的长,再利用平行四边形的周长公式即可求出![]() 的周长;
的周长;
②设点C的坐标为(x,![]() x +4),则CE=|x|,CD=|
x +4),则CE=|x|,CD=|![]() x+4|,利用三角形的面积公式结合△CDE的面积为
x+4|,利用三角形的面积公式结合△CDE的面积为![]() ,可得出关于x的方程,解之即可得出结论.
,可得出关于x的方程,解之即可得出结论.
解:(1)将A(8,0)代入y=kx+4,得:0=8k+4,
解得:k=![]() .故答案为:
.故答案为:![]() .
.
(2)①由(1)可知直线AB的解析式为y=![]() x+4.
x+4.
当x=0时,y=![]() x+4=4,∴点B的坐标为(0,4),
x+4=4,∴点B的坐标为(0,4),
∴OB=4.
∵点E为OB的中点,∴BE=OE=![]() OB=2.
OB=2.
∵点A的坐标为(8,0),∴OA=8.
∵四边形OCED是平行四边形,
∴CE∥DA,
∴![]() ,∴BC=AC,
,∴BC=AC,
∴CE是△ABO的中位线,∴CE=![]() OA=4.
OA=4.
∵四边形OCED是平行四边形,
∴OD=CE=4,OC=DE.
在Rt△DOE中,∠DOE=90°,OD=4,OE=2,
∴DE=![]() ,
,
∴![]() =2(OD+DE)=2(4+2
=2(OD+DE)=2(4+2![]() )=8+4
)=8+4![]() .
.
②如图,设点C的坐标为(x,![]() x +4),则CE=|x|,CD=|
x +4),则CE=|x|,CD=|![]() x+4|,
x+4|,
∴S△CDE=![]() CDCE=|﹣
CDCE=|﹣![]() x2+2x|=
x2+2x|=![]() ,
,
∴x2+8x+33=0或x2+8x﹣33=0.
方程x2+8x+33=0无解;
解方程x2+8x﹣33=0,
解得:x1=﹣3,x2=11,
∴点C的坐标为(﹣3,![]() )或(11,
)或(11,![]() ).
).


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】“童舒”童装商场某种童装进价为每件60元,当售价为每件100元时,每天可卖出120件:童装的售价每上涨1元,则每天少卖2件.为了让利于顾客,商场规定销售这种重装时利润率不能超过90%,则当每件童装的售价定为多少元时,商场销售此种童装时每天可获得最大利润?每天的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
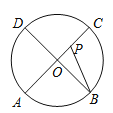
【题目】如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
A. 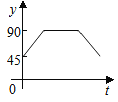 B.
B. 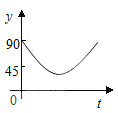 C.
C. 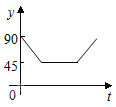 D.
D. 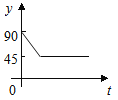
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )

A. 24° B. 33° C. 42° D. 43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“每天锻炼一小时,健康生活一辈子”.为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分 | 7 | 8 | 9 | 10 |
人数/人 | 2 | 5 | 4 | 4 |
(1)这组数据的众数是多少,中位数是多少.
(2)已知获得2018年四川省南充市的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 和直线y=(k+1)x+(k+1)2.
和直线y=(k+1)x+(k+1)2.
(1)求证:无论k取何值,抛物线总与x轴有两个不同的交点;
(2)如果抛物线与x轴的交点A,B在原点的右边,直线与x轴的交点C在原点的左边,又抛物线、直线分别交y轴于点D,E,直线AD交直线CE于点G(如图),且CAGE=CGAB,求抛物线的解析式.
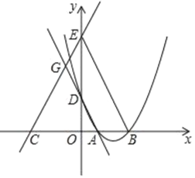
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种汽车刹车后行驶的距离s(单位:m)关于行驶的时间t(单位:s)的函数关系式为s=15t-at2,且t=1时,s=9.
(1)求s与t的函数关系式;
(2)该汽车刹车后到停下来前进了多远?
(3)该汽车刹车后前进6m时行驶了多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com