
分析 先由题意得出不等关系即他给父母买礼品的资金>500元但<550元,从而列出不等式组,即可解决问题.
解答 解:设买衣服a件,则买鞋(50-a)双,
则由给父母买礼品的资金>500元但<550元可得:$\left\{\begin{array}{l}{2500-45a-25(50-a)<550}\\{500<2500-45a-25(50-a)}\end{array}\right.$,
解得:35<a<37.5,
所以a=36或37,
即①买衣服36件,买鞋14双;
②买衣服37件,买鞋13双.
答:有两种方案即:买衣服36件,买鞋14双;买衣服37件,买鞋13双.
点评 本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式组或方程组即可求解.


科目:初中数学 来源: 题型:解答题
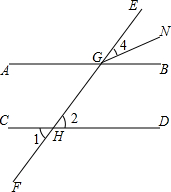
 已知:如图∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.
已知:如图∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
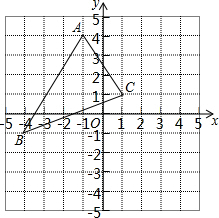 如图,若△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0-3),那么将△ABC作同样的平移得到△A1B1C1,则点A的对应点A1的坐标是( )
如图,若△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0-3),那么将△ABC作同样的平移得到△A1B1C1,则点A的对应点A1的坐标是( )| A. | (4,1) | B. | (9,-4) | C. | (-6,7) | D. | (-1,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
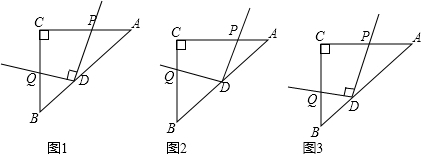
 下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整:
下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com