
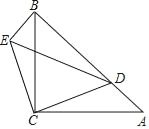
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=3![]() ,点D在AB上,且BD=2AD,连接CD,将线段CD绕点C逆时针方向旋转90°至CE,连接BE,DE.
,点D在AB上,且BD=2AD,连接CD,将线段CD绕点C逆时针方向旋转90°至CE,连接BE,DE.
(1)求证:△ACD≌△BCE;
(2)求线段DE的长度.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)先根据旋转的性质,由线段CD绕点C逆时针旋转90°,于是可得∠ACD=∠BCE,然后根据SAS即可得到△ACD≌△BCE;(2)先在RT△中利用勾股定理求出AB=6,由BD=2AD得到AD=2,BD=4,再证明∠DBE=90°,BE=2,然后在RT△BDE中利用勾股定理即可求出DE的长度.
详解:(1)证明:∵将线段CD绕点C逆时针方向旋转90°至CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠ACB﹣∠BCD=∠DCE﹣∠BCD,
即∠ACD=∠BCE.
在△ACD与△BCE中,
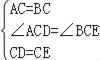 ,
,
∴△ACD≌△BCE;
(2)解:∵在Rt△ABC中,∠C=90°,AC=BC=3![]() ,
,
∴AB=6.
∵BD=2AD,
∴AD=2,BD=4.
由(1)可知△ACD≌△BCE,
∴∠CBE=∠A=45°,BE=AD=2,
∴∠DBE=∠ABC+∠CBE=90°.
∵在Rt△BDE中,∠DBE=90°,
∴DE2=BE2+BD2,
∴DE=![]() =2
=2![]() .
.
点睛:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质,勾股定理等知识.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】两组数据:98,99,99,100和98.5,99,99,99.5,则关于以下统计量说法不正确的是( )
A. 平均数相等
B. 中位数相等
C. 众数相等
D. 方差相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买![]() 双运动鞋,建议购买
双运动鞋,建议购买![]() 号运动鞋 双.
号运动鞋 双.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
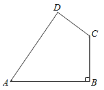
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD等于( )
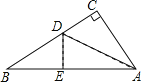
A. 3cmB. 4cmC. 5cmD. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若 ![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 的距离
的距离![]() 倍,我们就称点
倍,我们就称点![]() 是
是![]() 的巧点.若
的巧点.若 ![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到 ![]() 的距离一半,我们就称点
的距离一半,我们就称点![]() 是
是![]() 的妙点.如图,点
的妙点.如图,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,表示
,表示![]() 的点
的点![]() 到点
到点![]() 的距离是
的距离是![]() ,到点
,到点![]() 的距离是
的距离是![]() ,那么点
,那么点![]() 是
是![]() 的巧点,点
的巧点,点![]() 是
是![]() 的妙点.
的妙点.
![]()
知识运用:
(1)如图 1,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,那么点
,那么点![]() 是(
是(![]() 的( )
的( )
![]()
A.巧点 B. 妙点 C. 无法确定
(2)如图 2,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为
所表示的数为![]() ,则(
,则(![]() 的巧点表示的数是 ;
的巧点表示的数是 ;
![]()

拓展提升
(3)如图 3,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为
所表示的数为![]() .现有一只电子蚂蚁P从点
.现有一只电子蚂蚁P从点 ![]() 出发,以每
出发,以每![]() 秒单位的速度向右运动,到达点
秒单位的速度向右运动,到达点![]() 停止. 当经过几秒时,
停止. 当经过几秒时,![]() 和
和 ![]() 其有一个点为其余两点的巧点? (请直接写出结果)
其有一个点为其余两点的巧点? (请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出发,沿一条直道跑步,经过一段时间原路返回,刚好在第16分钟回到家中.设小明出发第t分钟的速度为v米/分,离家的距离为s米.v与t之间的部分图象、s与t之间的部分图象分别如图1与图2(图象没画完整,其中图中的空心圈表示不包含这一点),则当小明离家600米时,所用的时间是( )分钟.

A. 4.5B. 8.25C. 4.5 或8.25D. 4.5 或 8.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青竹湖湘一外国语学校初![]() 级全体学生从学校统一乘车去市科技馆参观学习,然后又统一乘车原路返回,需租用客车若干辆.现有甲、乙两种座位数相同的客车可以租用,甲种客车每辆的租金为
级全体学生从学校统一乘车去市科技馆参观学习,然后又统一乘车原路返回,需租用客车若干辆.现有甲、乙两种座位数相同的客车可以租用,甲种客车每辆的租金为![]() 元,另按实际行程每千米加收
元,另按实际行程每千米加收![]() 元;乙种客车每辆按每千米
元;乙种客车每辆按每千米![]() 元收费.
元收费.
(1)当行程为多少千米时,租用两种客车的费用相同?
(2)青竹湖湘一外国语学校距市科技馆约![]() 公里,如果你是年级组杨组长,为节省费用,你会选择哪种客车?
公里,如果你是年级组杨组长,为节省费用,你会选择哪种客车?
查看答案和解析>>
科目:初中数学 来源: 题型:
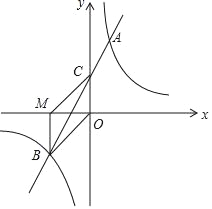
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com