
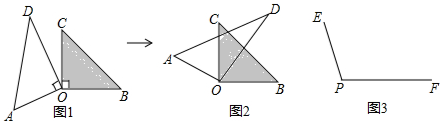
分析 (1)根据周角的定义得到∠AOB=360°-90°-90°-20°=160°,根据角的和差得到∠AOC=∠BOD,;
(2)根据余角的性质即可得到结论;
(3)过P作PM⊥PF,PN⊥PE,则∠MPN即为所求.
解答 解:(1)∵∠AOD=∠BOC=90°,∠COD=20°,
∴∠AOB=360°-90°-90°-20°=160°,
∵∠AOC=90°+∠COD=110°,∠BOD=90°+∠COD=110°,
∴∠AOC=∠BOD,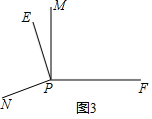
∴图中以O为顶点的相等的角(除直角外)还有:∠AOC=∠BOD;
故答案为:160,∠AOC,∠BOD;
(2)由图1到图2,∠DOC经历了先变小再变大的过程,则下列叙述:
①∠COD变小时,∠AOB变大;正确;
②∠COD变小时,∠AOB变大;错误;
③总是∠AOC=∠BOD;正确;
④总是∠COD+∠AOB=180°;正确;
⑤当OD平分∠COB时,OC也平分∠AOD.正确.
其中正确的是(D);
(3)如图所示.
点评 本题考查了角的计算,余角和补角,正确的识别图形是解题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
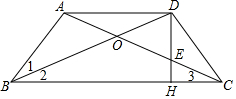 如图,已知四边形ABCD中,AC与BD相交于点O,OA=OD,∠1=∠2=∠3,∠BAC=90°,DH⊥BC于H,DH交AC于E.
如图,已知四边形ABCD中,AC与BD相交于点O,OA=OD,∠1=∠2=∠3,∠BAC=90°,DH⊥BC于H,DH交AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
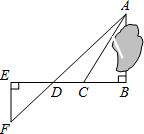 为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.根据所测数据,能出A,B间距离的有①②③(填上所有能求出A、B间距离的序号)
为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.根据所测数据,能出A,B间距离的有①②③(填上所有能求出A、B间距离的序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com