Question

【题目】如图，经过点A（0，﹣4）的抛物线y=x2+bx+c与x轴相交于点B（﹣1，0）和C，O为坐标原点．

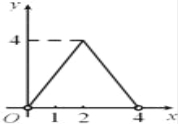
（1）求抛物线的解析式；

（2）将抛物线y=x2+bx+c向上平移个单位长度，再向左平移m（m＞0）个单位长度，得到新抛物线，若新抛物线的顶点P在△ABC内，求m的取值范围；

（3）将x轴下方的抛物线图象关于x轴对称，得到新的函数图象C，若直线y=x+k与图象C始终有3个交点，求满足条件的k的取值范围．

Answer 1

【答案】(1)、y=；(2)、＜m＜；(3)、1或

【解析】

试题分析：(1)、该抛物线的解析式中只有两个待定系数，只需将A、B两点坐标代入即可得解．(2)、首先根据平移条件表示出移动后的函数解析式，进而用m表示出该函数的顶点坐标，将其代入直线AB、AC的解析式中，即可确定P在△ABC内时m的取值范围．(3)、先根据函数解析式画出图形，然后结合图形找出抛物线与x轴有三个交点的情形，最后求得直线的解析式，从而可求得m的值．

试题解析：(1)、∵经过点A（0，﹣4）的抛物线y=x2+bx+c与x轴相交于点B（﹣1，0），

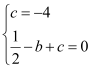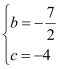∴， ∴， ∴抛物线解析式为y=x2﹣x﹣4，

(2)、由(1)知，抛物线解析式为yx2﹣x﹣4=（x2﹣7x）﹣4=（x﹣）2﹣，

∴此抛物线向上平移个单位长度的抛物线的解析式为y=（x﹣）2﹣，

再向左平移m（m＞0）个单位长度，得到新抛物线y=（x+m﹣）2﹣，

∴抛物线的顶点P（﹣m+，﹣）， 对于抛物线y=x2﹣x﹣4，令y=0， x2﹣x﹣4=0，解得x=﹣1或8， ∴B（8，0），∵A（0，﹣4），B（﹣1，0），

∴直线AB的解析式为y=﹣4x﹣4，直线AC的解析式为y=x﹣4， 当顶点P在AB上时，﹣ =﹣4×（﹣m+）﹣4，解得m=， 当顶点P在AC上时，﹣ =（﹣m+）﹣4，

解得m=， ∴当点P在△ABC内时＜m＜．

(3)、翻折后所得新图象如图所示．

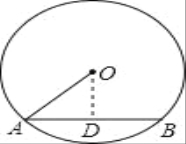
平移直线y=x+k知：直线位于l1和l2时，它与新图象有三个不同的公共点．

①当直线位于l1时，此时l1过点B（﹣1，0）， ∴0=﹣1+k，即k=1．

②∵当直线位于l2时，此时l2与函数y=﹣x2+x+4（﹣1≤x≤8）的图象有一个公共点

∴方程x+k=﹣x2+x+4，即x2﹣5x﹣8+2k=0有两个相等实根． ∴△=25﹣4（2k﹣8）=0，即k=．

综上所述，k的值为1或．