
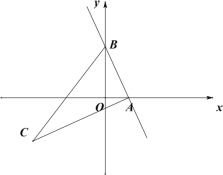
【题目】如图所示,已知直线![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 与点
与点![]() ,点
,点![]() 在第三象限内,且
在第三象限内,且![]() ,
,![]() .
.
(1)当![]() 时,求抛物线的表达式;
时,求抛物线的表达式;
(2)设点![]() 坐标为
坐标为![]() ,试用
,试用![]() 分别表示
分别表示![]() ;
;
(3)记![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)8
;(3)8
【解析】
(1)把A、B两点代入可求得结果;
(2)作CH⊥![]() 轴,构造直角三角形,根据
轴,构造直角三角形,根据![]() 找到已知边的关系,进而求得结果;
找到已知边的关系,进而求得结果;
(3)由A、C两点可得到关于x、y的式子,代入计算即可.
解:(1)当![]() 时,
时,![]() ,
,![]() ;
;
抛物线![]() 经过点
经过点![]() 与点
与点![]() ;
;
∴所求抛物线的表达式为![]() ;
;
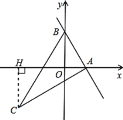
(2)如图:作CH⊥![]() 轴,垂足为点H,得∠AHC=∠AOB=90°;
轴,垂足为点H,得∠AHC=∠AOB=90°;
∵AC⊥AB,
∴∠OAB+∠CAH=90°,
又∵∠CAH+∠ACH=90°,
∴∠OAB=∠ACH;
∴△AOB∽△CHA,
∴![]() ;
;
∵tan∠ABC=![]() ,
,
∴![]() ;
;
∵OA=![]() ,OB=2,
,OB=2,
∴CH=2![]() ,AH=4;
,AH=4;
∴点C的坐标为(![]()
![]() 4,
4,![]() 2
2![]() ).
).
∴![]() .
.
(3)由点![]() 在
在![]() 轴的正半轴上,点C(
轴的正半轴上,点C(![]()
![]() 4,
4,![]() 2
2![]() )在第三象限内得
)在第三象限内得![]() ;
;
∴![]()
![]() =
=![]() (
(![]() );
);
∴当![]() =2时
=2时![]() 取得最大值8.
取得最大值8.


科目:初中数学 来源: 题型:
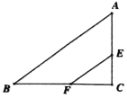
【题目】如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,点E、F分别是边AC、BC上的动点,且EF//AB,点C关于EF的对称点D恰好落在△ABC的内角平分线上,则CD长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在8×6的方格纸ABCD中,AB=6,每个小方格纸的顶点为格点,请按要求画出格点多边形,且所画格点多边形的顶点均不与点A,B,C,D重合.
(1)在图1中画一个格点三角形EFG,使得点E,F,G分别在AB,BC,AD上,且∠EFG=90°,
(2)在图2中画一个四边形EFGH,使点F为边BC的中点,E,G,H分别落在边AB,CD,DA上,且EG⊥FH,∠AEG≠90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现
如图1,在边长为1的正方形网格中,连接格点![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中![]() 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点
不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点![]() 、
、![]() ,可得
,可得![]() ,则
,则![]() ,连接
,连接![]() ,那么
,那么![]() 就变换到中
就变换到中![]() .
.
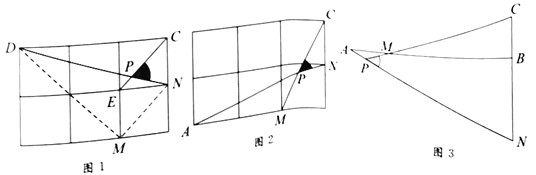
问题解决
(1)直接写出图1中![]() 的值为_________;
的值为_________;
(2)如图2,在边长为1的正方形网格中,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值;
的值;
思维拓展
(3)如图3,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,用上述方法构造网格求
,用上述方法构造网格求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在C处看到西北方向上有一凉亭A,北偏东![]() °的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=
°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=![]() 米,则A、B两点相距 ( )
米,则A、B两点相距 ( )
A.![]() 米B.
米B.![]() 米
米
C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着疫情的有效控制我省百大项目之一的哈尔滨地铁“二号线三号线”全面复工修建,建设方通过合理化地施工设计,加大适当的投入来弥补前期耽误的工作量,以保证今年修建目标的实现。修建过程中有大量的残土需要运输。某车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次可以运输110吨残土.
(1)求该车队有载重量为8吨、10吨的卡车各多少辆?
(2)随着工程的进展,该车队需要一次运输残土不低于165吨,为了完成任务,该车队准备新购进这两种卡车共6辆,则最多购进载重量为8吨的卡车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com