
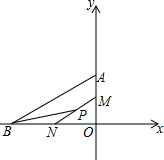
 如图,在平面直角坐标系中,点A的坐标为(0,5),点B的坐标为(-8,0),点M从点A出发沿AO以每秒1个单位长度的速度运动至点O,同时点N从点B出发沿射线BO以每秒2个单位长度的速度运动,当点M运动至O时,点N也同时停止运动,P是MN的中点,连接BP,设点M的运动时间为t(s).
如图,在平面直角坐标系中,点A的坐标为(0,5),点B的坐标为(-8,0),点M从点A出发沿AO以每秒1个单位长度的速度运动至点O,同时点N从点B出发沿射线BO以每秒2个单位长度的速度运动,当点M运动至O时,点N也同时停止运动,P是MN的中点,连接BP,设点M的运动时间为t(s).分析 (1)由时间=路程÷速度,可得出当M点运动到O点时的时间,结合N点的运动速度,即可得出结论;
(2)过点P作PC⊥x轴交x轴于点C,过点P作PD⊥y轴交y轴于点D,用含t的代数式表示出来MO和NO,由P为MN的中点得出PC、PD为△MON的中位线,从而得到P点的坐标,令P点的横坐标为0,即可算出P在y轴上时运动的时间t;
(3)线段BN和MN将△AOB分成了三部分,除了四边形ABPM外还有两个三角形,用△AOB的面积减去两个小三角形的面积即可得出S与t的函数关系式,令S=11,结合0<t<4即可得出结论.
解答 解:(1)∵点A的坐标为(0,5),点B的坐标为(-8,0),
∴AO=5,BO=8.
当运动刚好停止时,运动的时间t=5÷1=5,
此时点N运动的路程为2×5=10,10-8=2,即点N的坐标为(2,0).
故答案为:(2,0).
(2)过点P作PC⊥x轴交x轴于点C,过点P作PD⊥y轴交y轴于点D,如图所示.
∵AM=t,BN=2t,AO=5,BO=8,
∴MO=5-t,NO=8-2t,
∵P为MN的中点,
∴PD、PC均为△OMN的中位线,
∴PD=4-t,PC=$\frac{5-t}{2}$,
∴点P的坐标为(t-4,$\frac{5-t}{2}$).
令t-4=0,解得:t=4,
∴当t=4时,点P在y轴上.
(3)由题意可知:
S=$\frac{1}{2}$BO•AO-$\frac{1}{2}$MO•NO-$\frac{1}{2}$BN•PC,
=$\frac{1}{2}$×5×8-$\frac{1}{2}$×(5-t)×(8-2t)-$\frac{1}{2}$×$\frac{5-t}{2}$×2t,
=-$\frac{1}{2}$t2+$\frac{13}{2}$t,
∴S与t的函数关系式为S=-$\frac{1}{2}$t2+$\frac{13}{2}$t(0<t<4).
令S=11,即-$\frac{1}{2}$t2+$\frac{13}{2}$t=11,
解得:t=2,或t=11(舍去),
∴当t=2时,四边形ABPM的面积为11.
点评 本题考查了一次函数的应用、中位线的性质以及三角形的面积公式,解题的关键:(1)算出停止运动时的时间;(2)利用中位线的性质找出P点的坐标;(3)分割三角形AOB.本题属于中档题,难度不大,(1)较简单;(2)初中没有学到中点坐标,但是在日常做题中常常用到,此处如果用中点坐标公式会更简洁一些;(3)分割图形求面积是我们求不规则图形面积时常用到的手段,在日常学习中应加强学生对分割图形求面积的练习.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
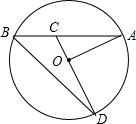 如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD.
如图,已知AB是⊙O的弦,OA=4,∠A=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com