
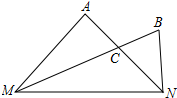
 如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )| A. | 若α=β,则点C在MN的垂直平分线上 | |
| B. | 若α+β=180°,则∠AMB=∠NMB | |
| C. | ∠MCN=$(\frac{α+β}{3}+60)$° | |
| D. | 当∠MCN=120°时,延长MA、NB交于点O,则OA=OB |
分析 A.若α=β,易得∠AMC=∠BNC,由角平分线的性质易得∠CMN=∠CNM,由等腰三角形的性质,可得CM=CN,利用垂直平分线的判定定理可得结论;
B、BM平分∠AMN,即∠AMB=∠NMB,与α、β无关;
C、由三角形内角和等于180°易得∠A+∠AMN+∠ANM=180°和∠B+∠BMN+∠BNM=180°,由角平分线定义可知∠AMN=2∠BMN和∠BNM=2∠ANM,套入前面两等式相加可得出∠BMN+∠ANM=120°-$\frac{α+β}{3}$,在△CMN中由三角形内角和为180°即可得出结论;
D、当∠MCN=120°时,延长MA、NB交于点O,只能得出∠MON=60°,从而得出D答案不成立.
解答 答:A、∵α=β,∠MCA=∠NCB,
∴△MCA∽△NCB,
∴∠AMC=∠BNC,
∵BM平分∠AMN,AN平分∠BNM,
∴∠MNC=∠CNM,
∴点C在MN的垂直平分线上.
即A成立;
B、∵BM平分∠AMN,
∴∠AMB=∠NMB.
即B成立;
C、∵∠A+∠AMN+∠ANM=180°,∠B+∠BMN+∠BNM=180°,且BM平分∠AMN,AN平分∠BNM,
∴∠A+2∠BMN+∠ANM=180°,∠B+∠BMN+2∠ANM=180°,
,两式相加得:∠A+2∠BMN+∠ANM+∠B+∠BMN+2∠ANM=360°,
即α°+β°+3(∠BMN+∠ANM)=360°,
∴∠BMN+∠ANM=120°-$\frac{α+β}{3}$°.
由三角形的内角和为180°可知:∠BMN+∠ANM+∠MCN=180°,
∴∠MCN=(60+$\frac{α+β}{3}$)°.
即C成立;
由排除法可知D选项不成立.
故选D.
点评 本题考查了角平分线的定义、相似三角形的判定及性质和三角形的内角和为180°,解题的关键是逐项分析选项得知A、B、C均成立.本题属于中档题,在各选项的判断中用到的知识点较多,唯一的好处在于本题是选择题,不需要去证明和验证各项结论.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
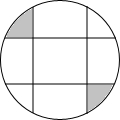 如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )
如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )| A. | $\sqrt{2}$π | B. | 2-π | C. | π | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
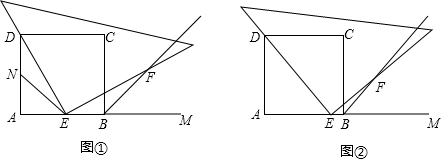
 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
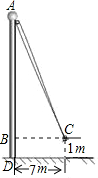 如图1,小红将升旗的绳子拉到旗杆顶端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆7m处,发现此时绳子末端距离地面1m,则绳子的长度为( )
如图1,小红将升旗的绳子拉到旗杆顶端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆7m处,发现此时绳子末端距离地面1m,则绳子的长度为( )| A. | 25m | B. | 4m | C. | 16m | D. | 17m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
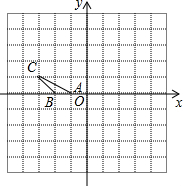 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),| A. | (-1,1) | B. | (2,3) | C. | (4,1) | D. | (0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com