
【题目】如图①,在正方形![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() .
.
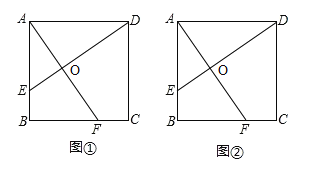
(1)试探索线段![]() 、
、![]() 的关系,写出你的结论并说明理由;
的关系,写出你的结论并说明理由;
(2)连接![]() 、
、![]() ,分别取
,分别取![]() 、
、![]() 、
、![]() 、
、![]() 的中点
的中点![]() 、
、![]() 、
、![]() 、
、![]() ,四边形
,四边形![]() 是什么特殊平行四边形?请在图②中补全图形,并说明理由.
是什么特殊平行四边形?请在图②中补全图形,并说明理由.
【答案】(1)AF=DE,AF⊥DE,理由见详解;(2)四边形HIJK是正方形,补图、理由见详解.
【解析】
(1)根据已知利用SAS判定△DAE≌△ABF,由全等三角形的判定方法可得到AF=DE,∠BAF=∠ADE,再由直角三角形的两个锐角互余和有两个角互余的三角形是直角三角形可证得AF⊥DE.
(2)根据已知可得HK,KJ,IJ,HI都是中位线,由全等三角形的判定可得到四边形四边都相等且有一个角是直角,从而来可得到该四边形是正方形.
解:(1)AF=DE, AF⊥DE.
∵ABCD是正方形,
∴AB=AD,∠DAB=∠ABC=90°,
∵AE=BF,
∴△DAE≌△ABF,
∴AF=DE,∠BAF=∠ADE.
∵∠DAB=90°,
∴∠BAF+∠DAF=90°,
∴∠ADE+∠DAF=90°,
∴AF⊥DE.
∴AF=DE,AF⊥DE.
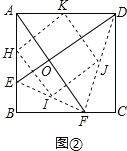
(2)四边形HIJK是正方形.
如下图,H、I、J、K分别是AE、EF、FD、DA的中点,
∴HI=KJ=![]() AF,HK=IJ=
AF,HK=IJ=![]() ED,
ED,
∵AF=DE,
∴HI=KJ=HK=IJ,
∴四边形HIJK是菱形,
∵△DAE≌△ABF,
∴∠ADE=∠BAF,
∵∠ADE+∠AED=90°,
∴∠BAF+∠AED=90°,
∴∠AOE=90°
∴∠KHI=90°,
∴四边形HIJK是正方形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
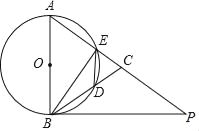
【题目】在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,P为AC延长线上一点,且∠PBC=![]() ∠BAC,连接DE,BE.
∠BAC,连接DE,BE.
(1)求证:BP是⊙O的切线;
(2)若sin∠PBC=![]() ,AB=10,求BP的长.
,AB=10,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蔬菜基地种植了娃娃菜和油菜两种蔬菜共![]() 亩,设种植娃娃菜
亩,设种植娃娃菜![]() 亩,总收益为
亩,总收益为![]() 万元,有关数据见下表:
万元,有关数据见下表:
成本(单位:万元/亩) | 销售额(单位:万元/亩) | |
娃娃菜 | 2.4 | 3 |
油菜 | 2 | 2.5 |
(1)求![]() 关于
关于![]() 的函数关系式(收益 = 销售额 – 成本);
的函数关系式(收益 = 销售额 – 成本);
(2)若计划投入的总成本不超过![]() 万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
(3)已知娃娃菜每亩地需要化肥![]() kg,油菜每亩地需要化肥
kg,油菜每亩地需要化肥![]() kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的
kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的![]() 倍,结果运送完全部化肥的次数比原计划少
倍,结果运送完全部化肥的次数比原计划少![]() 次,求基地原计划每次运送多少化肥.
次,求基地原计划每次运送多少化肥.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E分别是不等边△ABC(即AB,BC,AC互不相等)的边AB,AC的中点.点O是△ABC所在平面上的动点,连接OB,OC,点G,F分别是OB,OC的中点,顺次连接点D,G,F,E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
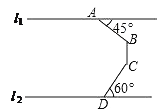
【题目】如图,在同一平面内,两条平行景观长廊l1和l2间有一条“U”形通道,其中AB段与景观长廊l1成45°角,长为20m;BC段与景观长廊垂直,长为10m,CD段与景观长廊l2成60°角,长为10m,求两景观长廊间的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.
(1)求证:△ADE∽△BEC.
(2)若AD=1,BC=3,AE=2,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com