已知...- 依据上述规律.计算的结果为题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

已知，，，…

依据上述规律，计算的结果为　　（写成一个分数的形式）

。

【考点】探索规律题（数字的变化类），分式的化简计算。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

如图，Rt△ABC中，∠ACB=90°，AC=BC=4cm，CD=1cm，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，至A点结束，设E点的运动时间为t秒，连接DE，当△BDE是直角三角形时，t的值为秒。

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，在△ABC中，AB=AC，D是BA延长线上的一点，点E是AC的中点．

（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应字母（保留作图痕迹，不写作法）．

①作∠DAC的平分线AM． ②连接BE并延长交AM于点F．

（2）猜想与证明：试猜想AF与BC有怎样的位置关系和数量关系，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

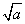
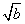
阅读理解：对于任意正实数a、b，∵(－)²≥0，∴a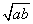－2＋b≥0，∴a＋b≥2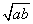，只有当a＝b时，等号成立.

结论：在a＋b≥2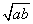（a、b均为正实数）中，若ab为定值p，则a+b≥2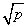，只有当a＝b时，a＋b有最小值2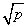. 根据上述内容，回答下列问题：

（1）若m＞0，只有当m＝时，m＋有最小值；

若m＞0，只有当m＝时，2m＋有最小值 .

（2）如图，已知直线L₁：y＝x＋1与x轴交于点A，过点A的另一直线L₂与双曲线y＝

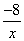
（x>0）相交于点B（2，m），求直线L₂的解析式.

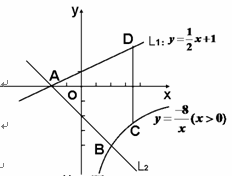
（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L₁于点D，试

求当线段CD最短时，点A、B、C、D围成的四边形面积.

查看答案和解析>>

科目：初中数学 来源： 题型：

观察数表

根据表中数的排列规律，则B+D=　　．

查看答案和解析>>

科目：初中数学 来源： 题型：

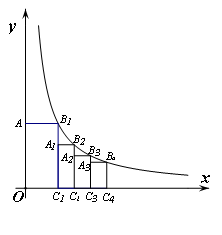
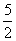
如图，点B₁在反比例函数y=（x＞0）的图象上，过点B₁分别作x轴和y轴的垂线，垂足为C₁和A，得到第一个矩形AOC₁B₁，点C₁的坐标为（1，0）；取x轴上一点C₂（，0），过点C₂作x轴的垂线交反比例函数图象于点B₂，过B₂作线段B₂ A₁⊥B₁C₁_，，交B₁C₁于点A₁，得到第二个矩形A₁C₁C₂B₂；依次在x轴上取点C₃（2，0），C₄（，0）按此规律作矩形，则第10个矩形A₉C₉C₁₀B₁₀的面积为．