
【题目】抛物线![]() 经过点E(5,5),其顶点为C点.
经过点E(5,5),其顶点为C点.
(1)求抛物线的解析式,并直接写出C点坐标.
(2)将直线![]() 沿y轴向上平移b个单位长度交抛物线于A、B两点.若∠ACB=90°,求b的值.
沿y轴向上平移b个单位长度交抛物线于A、B两点.若∠ACB=90°,求b的值.
(3)是否存在点D(1,a),使抛物线上任意一点P到x轴的距离等于P点到点D的距离?若存在,请求点D的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ,顶点(1,1)(2)
,顶点(1,1)(2)![]() (3)(1,2)
(3)(1,2)
【解析】
(1)将点E坐标代入解析式,求出系数a,获得解析式,并求出顶点C坐标;
(2)平移直线y=![]() ,获得平移后的解析式y=
,获得平移后的解析式y=![]() ,直线与抛物线交于两点A、B,设A(x1,y1)、B(x2,y2),因为∠ACB=90°,利用A、B、C三点构造相似,得到
,直线与抛物线交于两点A、B,设A(x1,y1)、B(x2,y2),因为∠ACB=90°,利用A、B、C三点构造相似,得到![]()
![]() ,将直线与抛物线联立获得方程,根据韦达定理,获得x1+x2,x1x2,从而获得关于b的方程,求出b值;
,将直线与抛物线联立获得方程,根据韦达定理,获得x1+x2,x1x2,从而获得关于b的方程,求出b值;
(3)过点P作PQ⊥x轴,设点P(m,![]() )因为PQ=PD,所以PQ2=PD2,整理可得
)因为PQ=PD,所以PQ2=PD2,整理可得![]() ,所以当a=2时,存在点D(1,2).
,所以当a=2时,存在点D(1,2).
(1)将点E(5,5)代入y=ax2-![]() +
+![]()
5=25a-![]() +
+![]()
a=![]()
∴y=![]() ,顶点(1,1)
,顶点(1,1)
(2)直线y=![]() 平移后获得解析式y=
平移后获得解析式y=![]()
交抛物线于A(x1,y1)、B(x2,y2)
y1=![]() ,y2=
,y2=![]()
联立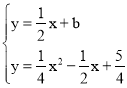
x2-4x+5-4b=0
∴x1+x2=4,x1x2=5-4b
如图,过点A、B作y轴的平行线与过点C平行于x轴的线交于点E,F
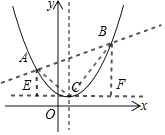
可证△ACE∽△BCF
∴![]() =
=![]()
∴(x1+x2)-(x1x2)-1=y1y2-(y1+y2)+1
∴b2-5b+![]() =0,
=0,
解,b1=![]() ,b2=
,b2=![]() (舍)
(舍)
∴b=![]() .
.
(3)设P(m,n),作PQ⊥x轴于Q
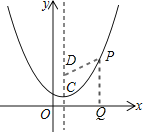
若PQ=PD,则PQ2=PD2
(m-1)2+(n-a)2=n2
整理得
m2-2m+1+a2-2an=0
将n=![]() 代入
代入
整理得![]()
当a=2时,方程成立
∴D(1,2)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车的速度是小明骑车速度的3倍.
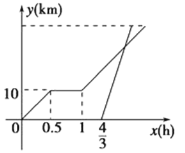
(1)求小明骑车的速度为 km/h.在甲地游玩的时间为 h.;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为2009年到2015年中关村国家自主创新示范区企业经营技术收入的统计图.下面四个推断:
①2009年到2015年技术收入持续增长;
②2009年到2015年技术收入的中位数是4032亿;
③2009年到2015年技术收入增幅最大的是2015年;
④2009年到2011年的技术收入增长的平均数比2013年到2015年技术收入增长的平均数大.
其中,正确的是( )
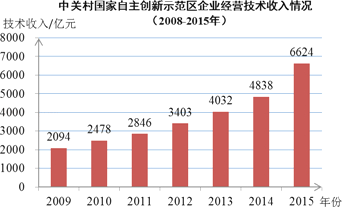
A.①③B.①④C.②③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对于随机事件的概率的描述:
①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”;
②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2;
③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85
其中合理的有______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和直线m,给出如下定义:若存在一点P,使得点P到直线m的距离等于1,则称P为直线m的平行点.
(1)当直线m的表达式为y=x时,
①在点![]() ,
,![]() ,
,![]() 中,直线m的平行点是______;
中,直线m的平行点是______;
②⊙O的半径为![]() ,点Q在⊙O上,若点Q为直线m的平行点,求点Q的坐标.
,点Q在⊙O上,若点Q为直线m的平行点,求点Q的坐标.
(2)点A的坐标为(n,0),⊙A半径等于1,若⊙A上存在直线![]() 的平行点,直接写出n的取值范围.
的平行点,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC=2,点P为BC边上的一个动点(不与点B,C重合).点P关于直线AC,AB的对称点分别为M,N,连接MN交AC于点E,交AB于点F.
(1)当点P为线段BC的中点时,求∠M的正切值.
(2)当点P在线段BC上运动时(不与B,C重合),连接AM,AN,求证:
①△AMN为等腰直角三角形;
②△AEF∽△BAM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某商店在2016年至2018年期间销售一种礼盒.2016年,该商店用2200元购进了这种礼盒并且全部售完:2018年,这种礼盒每盒的进价是2016年的一半,且该商店用2100元购进的礼盒数比2016年的礼盒数多100盒.那么,2016年这种礼盒每盒的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一束光线从y轴的点A(0,2)出发,经过x轴上的点C反射后经过点B(6,6),则光线从点A到点B所经过的路程是( )
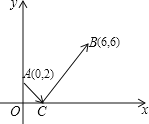
A.10B.8C.6D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于两个点
中,对于两个点![]() ,
,![]() 和图形
和图形![]() ,如果在图形
,如果在图形![]() 上存在点
上存在点![]() ,
,![]() (
(![]() ,
,![]() 可以重合),使得
可以重合),使得![]() ,那么称点
,那么称点![]() 与点
与点![]() 是图形
是图形![]() 的一对“倍点”.
的一对“倍点”.
已知![]() 的半径为1,点
的半径为1,点![]() .
.
(1)①点![]() 到
到![]() 的最大值,最小值;
的最大值,最小值;
②在![]() ,
,![]() ,
,![]() 这三个点中,与点
这三个点中,与点![]() 是
是![]() 的一对“倍点”的是_____;
的一对“倍点”的是_____;
(2)在直线![]() 上存在点
上存在点![]() 与点
与点![]() 是
是![]() 的一对“倍点”,求
的一对“倍点”,求![]() 的取值范围;
的取值范围;
(3)正方形![]() 的顶点
的顶点![]() ,
,![]() ,若正方形上的所有点与点
,若正方形上的所有点与点![]() 都是
都是![]() 的一对“倍点”,直接写出
的一对“倍点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com