
 ��ͼ������OABC������OA��OC�ֱ���x��y����������ϣ���B������Ϊ��3��2��������������y=$\frac{k}{x}$��k��0��x��0����ͼ����B��
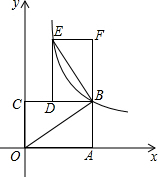
��ͼ������OABC������OA��OC�ֱ���x��y����������ϣ���B������Ϊ��3��2��������������y=$\frac{k}{x}$��k��0��x��0����ͼ����B������ ��1���ѵ�B��3��2�����뷴��������y=$\frac{k}{x}$�����k��ֵ���ɣ�
��2�����ɾ���OABC�����DEFB���ƣ��ó���DBE�ס�COB���ó���Ӧ����ȡ�DBE=��COB���ó���DBE+��CBO=90�㼴�ɣ�
���ɾ���OABC�����DEFB���ƣ��ó�DE��DB=OA��AB=3��2����DB=2k����DE=3k���ó���E�����꣬���뷴������������ʽ���ⷽ�����k��ֵ���ó�BD��DE�ij��������������DEFB�������
��� �⣺��1���ѵ�B��3��2�����뷴��������y=$\frac{k}{x}$�ã�k=6��
�෴���������Ľ���ʽΪ��y=$\frac{6}{x}$��
��2���١��ı���OABC�Ǿ��Σ�
���OCB=90�㣬
���COB+��CBO=90�㣬
�߾���OABC�����DEFB���ƣ�BD��DE��
���DBE�ס�COB��
���DBE=��COB��
���DBE+��CBO=90�㣬
����OBE=90�㣻
�ڡ߾���OABC�����DEFB���ƣ�
��DE��DB=OA��AB=3��2��
��DB=2k����DE=3k��CD=3-2k��AF=AB+DE=2+3k��
���E����������3-2k��2+3k����
�ѵ�E��3-2k��2+3k������y=$\frac{6}{x}$�ã�
��3-2k����2+3k��=6��
��ã�k=$\frac{5}{6}$��
��BD=2k=$\frac{5}{3}$��DE=3k=$\frac{5}{2}$��
�����DEFB�����=BD•DE=$\frac{5}{3}$��$\frac{5}{2}$=$\frac{25}{6}$��
���� �����Ƿ����������ۺ���Ŀ�������˷�������������ʽ����������ͼ�����������ƶ���Ρ����������ε����ʡ���������ļ����֪ʶ�������ۺ���ǿ����һ���Ѷȣ��������վ��ε����ʣ�ȷ����������������ʽ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
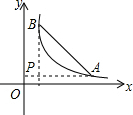 ��ͼ��A��BΪ����������λ�ڵ�һ������ͼ���ϵĵ㣬����A��x��Ĵ��������B��y�ᴹ�߽��ڵ�P�������ABPΪ����ֱ����������A������Ϊ��5��1�������ABP�����Ϊ8��
��ͼ��A��BΪ����������λ�ڵ�һ������ͼ���ϵĵ㣬����A��x��Ĵ��������B��y�ᴹ�߽��ڵ�P�������ABPΪ����ֱ����������A������Ϊ��5��1�������ABP�����Ϊ8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1��x��-$\frac{1}{2}$ | B�� | x��$\frac{1}{2}$ | C�� | x��-1 | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�������ϱ�ʾij����ʽ��Ľ⼯�����������ʽ������ǣ�������
��ͼ�������ϱ�ʾij����ʽ��Ľ⼯�����������ʽ������ǣ�������| A�� | $\left\{\begin{array}{l}{x��-2}\\{x��4}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{x��-2}\\{x��4}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{x��-2}\\{x��4}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{x��-2}\\{x��4}\end{array}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
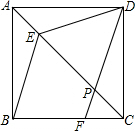 ��ͼ����������ABCD�У���E�ڶԽ���AC�ϣ���F�ڱ�BC�ϣ�����BE��DF��DF���Խ����ڵ�P����DE=DP��
��ͼ����������ABCD�У���E�ڶԽ���AC�ϣ���F�ڱ�BC�ϣ�����BE��DF��DF���Խ����ڵ�P����DE=DP���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com