
【题目】. 某工厂计划生产一批某种产品,数量不超过3500件. 该产品由![]() 三部分组成,分别由厂里甲、乙、丙三个车间完成. 三个车间于某天零时同时开工,每天24小时连续工作. 若干天后的零时,甲车间完成任务;几天后的18时,乙车间完成任务;自乙车间完成任务后的当天零时起,再过几天后的8时,丙车间完成任务. 已知三个车间每天完成
三部分组成,分别由厂里甲、乙、丙三个车间完成. 三个车间于某天零时同时开工,每天24小时连续工作. 若干天后的零时,甲车间完成任务;几天后的18时,乙车间完成任务;自乙车间完成任务后的当天零时起,再过几天后的8时,丙车间完成任务. 已知三个车间每天完成![]() 的数量分别为300件、240件、180件,该工厂完成这种产品的件数是___________.
的数量分别为300件、240件、180件,该工厂完成这种产品的件数是___________.
【答案】3300件
【解析】
设甲a天完成任务,乙(a+b+![]() )天完成任务,丙(a+b+c+
)天完成任务,丙(a+b+c+![]() )天完成任务,列出关于a,b,c的方程,得到a=4b+3,b=
)天完成任务,列出关于a,b,c的方程,得到a=4b+3,b=![]() ,再列出关于a,b,c的不等式,结合a,b,c为正整数,即可求出a,b,c的值,进而求出答案.
,再列出关于a,b,c的不等式,结合a,b,c为正整数,即可求出a,b,c的值,进而求出答案.
设甲a天完成任务,乙(a+b+![]() )天完成任务,丙(a+b+c+
)天完成任务,丙(a+b+c+![]() )天完成任务,
)天完成任务,
由题意得:300a=240×(a+b+![]() )=180×(a+b+c+
)=180×(a+b+c+![]() ),
),
∴5a=4a+4b+3=3a+3b+3c+1,解得:a=4b+3,b=![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,且a,b,c为正整数,
,且a,b,c为正整数,
∴当a=11时,b=2,c=5,当a=10 时,b不是整数,舍去,
同理,当a为其他正整数时,b,c不同时为正整数,
∴该工厂完成这种产品的件数是:11×300=3300(件).
故答案是:3300件.


科目:初中数学 来源: 题型:
【题目】为弘扬遵义红色文化,传承红色文化精神,某校准备组织学生开展研学活动.经了解,有A.遵义会议会址、B.苟坝会议会址、C.娄山关红军战斗遗址、D.四渡赤水纪念馆共四个可选择的研学基地.现随机抽取部分学生对基地的选择进行调查,每人必须且只能选择一个基地.根据调查结果绘制如下不完整的条形统计图和扇形统计图.
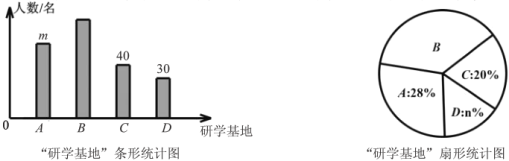
(1)统计图中![]() ______,
______,![]() ______;
______;
(2)若该校有1500名学生,请估计选择![]() 基地的学生人数;
基地的学生人数;
(3)某班在选择![]() 基地的6名学生中有4名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
基地的6名学生中有4名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
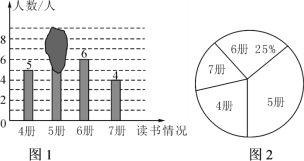
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形统计图(如图1)和不完整的扇形图(如图2),其中条形统计图被墨迹遮盖了一部分.
(1)求条形统计图中被遮盖的数,并写出册数的中位数;
(2)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没有改变,则最多补查了____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)若∠ADB=60°,BD=1,求阴影部分的面积.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点B,C在x轴上,反比例函数y=﹣![]() (x<0)的图象经过A,E两点,反比例函数y=
(x<0)的图象经过A,E两点,反比例函数y=![]() (x>0)的图象经过第一象限内的D,H两点,正方形EFCH的顶点F.G在AD上.已知A(﹣1,a),B(﹣4,0).
(x>0)的图象经过第一象限内的D,H两点,正方形EFCH的顶点F.G在AD上.已知A(﹣1,a),B(﹣4,0).
(1)求点C的坐标及k的值;
(2)直接写出正方形EFGH的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点
上的一个动点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)如图①,求证:![]() ;
;
(2)如图②,连接![]() 为
为![]() 的中点,
的中点,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 和
和![]() 的长;
的长;
(3)如图③,过点![]() 作
作![]() 于
于![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
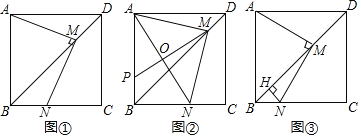
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com