
【题目】如图,平行四边形OABC的顶点O,B在y轴上,顶点A在反比例函数y=﹣![]() 上,顶点C在反比例函数y=
上,顶点C在反比例函数y=![]() 上,则平行四边形OABC的面积是( )
上,则平行四边形OABC的面积是( )
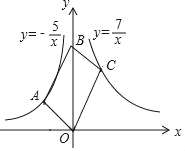
A.8B.10C.12D.![]()
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.
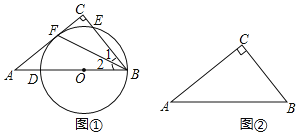
(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )

A. ![]() B.
B. ![]() C. 10D. 8
C. 10D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2ax+m.
(1)当a=2,m=﹣5时,求抛物线的最值;
(2)当a=2时,若该抛物线与坐标轴有两个交点,把它沿y轴向上平移k个单位长度后,得到新的抛物线与x轴没有交点,请判断k的取值情况,并说明理由;
(3)当m=0时,平行于y轴的直线l分别与直线y=x﹣(a﹣1)和该抛物线交于P,Q两点.若平移直线l,可以使点P,Q都在x轴的下方,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知![]() 米,
米,![]() 米,AB与水平线
米,AB与水平线![]() 的夹角是
的夹角是![]() ,BC与水平线
,BC与水平线![]() 的夹角是
的夹角是![]() .求:本次检修中,检修人员上升的垂直高度
.求:本次检修中,检修人员上升的垂直高度![]() 是多少米?(结果精确到1米,参考数据:
是多少米?(结果精确到1米,参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
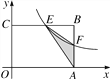
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某公司用800万元购得某种产品的生产技术后,进一步投入资金1550万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价需要定在200元到300元之间较为合理.销售单价![]() (元)与年销售量
(元)与年销售量![]() (万件)之间的变化可近似的看作是如下表所反应的一次函数:
(万件)之间的变化可近似的看作是如下表所反应的一次函数:
销售单价 | 200 | 230 | 250 |
年销售量 | 14 | 11 | 9 |
(1)请求出![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(2)请说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
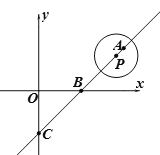
【题目】在平面直角坐标系中,直线y=x-2与x轴、y轴分别交于点B、C,半径为1的⊙P的圆心P从点A(4,m )出发以每秒![]() 个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t=_____秒时,⊙P与坐标轴相切.
个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t=_____秒时,⊙P与坐标轴相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
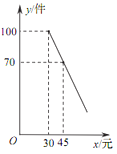
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com