
分析 (1)根据“神秘数”的定义,只需看能否把28和2012这两个数写成两个连续偶数的平方差即可判断;
(2)运用平方差公式进行计算,进而判断即可;
(3)运用平方差公式进行计算,进而判断即可.
解答 解:(1)是,理由如下:
∵28=82-62,2012=5042-5022,
∴28是“神秘数”;2012是“神秘数”;
(2)“神秘数”是4的倍数.理由如下:
(2k+2)2-(2k)2=(2k+2+2k)(2k+2-2k)=2(4k+2)=4(2k+1),
∴“神秘数”是4的倍数;
(3)设两个连续的奇数为:2k+1,2k-1,则
(2k+1)2-(2k-1)2=8k,
而由(2)知“神秘数”是4的倍数,但不是8的倍数,
所以两个连续的奇数的平方差不是神秘数.
点评 此题主要考查了平方差公式的应用,此题是一道新定义题目,熟练记忆平方差公式是解题关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
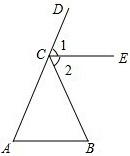 如图,给出下面3个论断:AB∥CE,∠1=∠2,∠A=∠B,请从中选取2个论断作为已知,另一个作为结论,组成一个真命题,并证明.
如图,给出下面3个论断:AB∥CE,∠1=∠2,∠A=∠B,请从中选取2个论断作为已知,另一个作为结论,组成一个真命题,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
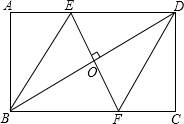 如图,在矩形ABCD中,边AB的长为3,点E、F,分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
如图,在矩形ABCD中,边AB的长为3,点E、F,分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )| A. | 2$\sqrt{3}$ | B. | $\frac{9}{2}$$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com