
【题目】某市计划建设一项水利工程,工程需要运送的土石方总量为![]() 米3,某运输公司承办了这项工程运送土石方的任务.
米3,某运输公司承办了这项工程运送土石方的任务.
(1)完成运送任务所需的时间![]() (单位:天)与运输公司平均每天的工作量
(单位:天)与运输公司平均每天的工作量![]() (单位:米3/天)之间具有怎样的函数关系?
(单位:米3/天)之间具有怎样的函数关系?
(2)已知这个运输公司现有50辆卡车,每天最多可运送土石方![]() 米3,则该公司完成全部运输任务最快需要多长时间?
米3,则该公司完成全部运输任务最快需要多长时间?
(3)运输公司连续工作30天后,天气预报说两周后会有大暴雨,公司决定10日内把剩余的土石方运完,平均每天至少增加多少辆卡车?
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
(1)求抛物线的解析式;
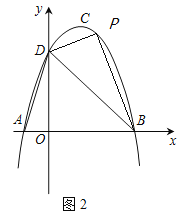
(2)如图2,点P为直线BD上方抛物线上一点,若![]() ,请求出点P的坐标.
,请求出点P的坐标.
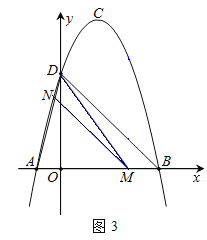
(3)如图3,M为线段AB上的一点,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,请求出点M的坐标.
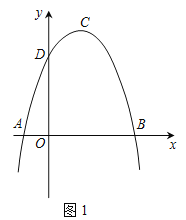
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是圆上一点,弦
是圆上一点,弦![]() 于点
于点![]() ,且
,且![]() .过点
.过点![]() 作
作![]() 的切线,过点
的切线,过点![]() 作
作![]() 的平行线,两直线交于点
的平行线,两直线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() 与
与![]() 相切;
相切;
(2)连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售一批衬衫,每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为了扩大 销售,决定采取适当的降价措施,经调查发现,如果一件衬衫每降价
元,为了扩大 销售,决定采取适当的降价措施,经调查发现,如果一件衬衫每降价![]() 元,每天 可多售出
元,每天 可多售出![]() 件。设每件衬衫降价
件。设每件衬衫降价![]() 元,每天盈利
元,每天盈利![]() 元.
元.
![]() 求出
求出![]() 与
与![]() 之间的函数关系式;(不需写自变量的取值范围).
之间的函数关系式;(不需写自变量的取值范围).
![]() 出每件衬衫降价多少元时,商场每天的盈利达到最大?盈利最大是多少元?
出每件衬衫降价多少元时,商场每天的盈利达到最大?盈利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
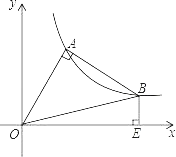
【题目】△OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y=![]() 正好过A,B两点,BE⊥x轴于E点,则OE2﹣BE2的值为( )
正好过A,B两点,BE⊥x轴于E点,则OE2﹣BE2的值为( )
A. 3B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三位正整数A与另一个三位正整数B相加得到三位数C,C的三个数位上的数字都相同,我们就称三位正整数A和三位正整数B互为“影子数”如:191+253=444,191+475=666…,所以191和253互为“影子数”,同时191和475也互为“影子数”,475和253都是191的“影子数”.
(1)若一个三位正整数M是67的倍数,它比它的一个“影子数”小107,求这个三位数M;
(2)若将一个三位正整数![]() 的十位和百位交换位置后组成的三位数是
的十位和百位交换位置后组成的三位数是![]() ,且
,且![]() 是
是![]() 的“影子数”,若
的“影子数”,若![]() ﹣
﹣![]() =540,求证:b=c+3.
=540,求证:b=c+3.
查看答案和解析>>
科目:初中数学 来源: 题型:
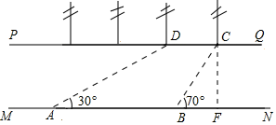
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂销售一种茶壶和茶杯,茶壶每只定价40元,茶怀每只定价5元.厂方在开展促销活动期间,向客户提供两种优惠方案:①茶壶和茶杯都按定价的90%付款;②买一个茶壶送一个茶杯.现某客户要到该厂购买![]() 个茶壶(
个茶壶(![]() ),茶杯个数是茶壶数的4倍少5.
),茶杯个数是茶壶数的4倍少5.
(1)若该客户按方案①购买,需付款______元(用含![]() 的代数式表示);若该客户按方案②购买.需付款______元;(用含
的代数式表示);若该客户按方案②购买.需付款______元;(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com