
【题目】如图1和2,四边形ABCD是菱形,点P是对角线AC上一点,以点P为圆心,PB为半径的弧,交BC的延长线于点F,连接PF,PD,PB.
(1)如图1,点P是AC的中点,请写出PF和PD的数量关系:;
(2)如图2,点P不是AC的中点,
①求证:PF=PD.
②若∠ABC=40°,直接写出∠DPF的度数.
【答案】
(1)PF=PD
(2)
解:①证明:
∵四边形ABCD是菱形,
∴AB=AD,∠BAC=∠DAC.
在△ABP和△ADP中,
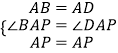 ,
,
∴△ABP≌△ADP(SAS),
∴PB=PD,
又∵PB=PF,
∴PF=PD.
②解:以P为圆心,PB为半径作圆P,则点B、F、D都在圆P上,连接BD.
由圆周角定理,可得∠DPF=2∠DBF,
又∵四边形ABCD是菱形,
∴∠ABC=2∠DBF,
∴∠DPF=∠ABC=40°.
【解析】(1)先根据菱形的对角线互相平分得出PB=PD,而由已知有PB=PF,则PF=PD;(2)①先由菱形的性质得出AB=AD,∠BAC=∠DAC,再由SAS证明△ABP≌△ADP,得出PB=PD,又PB=PF,则PF=PD;
②由于PB=PD=PF,以P为圆心,PB为半径作圆P,则点B、F、D都在圆P上,连接BD,则∠DPF=2∠DBF=∠ABC=40°.
【考点精析】本题主要考查了菱形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知:在△PAB的边PA、PB上分别取点C、D,连接CD使CD∥AB.将△PCD绕点P按逆时针方向旋转得到△PC′D′(∠APC′<∠APB),连接AC′、BD′.
(1)如图1, 若∠APB=90°,PA=PB,求证:AC′=BD′;AC′⊥BD′.
(2)在图1中,连接AD′、BC′,分别取AB、AD′、C′D′、BC′的中点E、F、G、H,顺次连接E、F、G、H得到四边形EFGH.请判断四边形EFGH的形状,并说明理由.
(3)①如图2, 若改变(1)中∠APB的大小,使0°<∠APB<90°,其他条件不变,重复(2)中操作.请你直接判断四边形EFGH的形状.
②如图3,若改变(1)中PA、PB的大小关系,使PA<PB,其他条件不变,重复(2)中操作,请你直接判断是四边形EFGH的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸每个小方格是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(a,b)D(1,4).
(1)描出A、B、C、D四点的位置.如图,则a= ;b= ;
(2)四边形ABCD的面积是 ;(直接写出结果)
(3)把四边形ABCD向左平移6个单位,再向下平移1个单位得到四边形A'B'C'D',在图中画出四边形A'B'C'D',并写出A'B'C'D'的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位计划用3天时间进行设备检修,安排小王,小李,小赵三位工程师各带班一天,带班顺序是随机确定的.
(1)请你写出三天带班顺序的所有可能的结果;
(2)求小李和小赵恰好相邻的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折线AC﹣BC是一条公路的示意图,AC=8km,甲骑摩托车从A地沿这条公路到B地,速度为40km/h,乙骑自行车从C地到B地,速度为10km/h,两人同时出发,结果甲比乙早到6分钟.
(1)求这条公路的长;
(2)设甲乙出发的时间为t小时,求甲没有超过乙时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
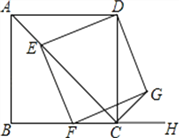
【题目】如图,已知四边形ABCD为正方形,AB=![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD= ![]() ,④S△ODC=S四边形BEOF中,正确的有( )
,④S△ODC=S四边形BEOF中,正确的有( ) 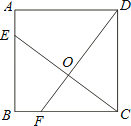
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com