
| A. | 方程x2+x-2=0有一根为-1 | |
| B. | 方程x2+x=0有一根为1 | |
| C. | 方程x2+3x-4=0有两个不相等的实数根 | |
| D. | 方程x2+4=0有两个实数根,并且这两根互为相反数 |
分析 A、把-1代入原方程即可得到结果;B、把1代入原方程即可得到结果;C、根据一元二次方程根的判别式即可进行判断;D、根据一元二次方程根的判别式和根与系数的关系即可进行判断.
解答 解:A、把-1代入x2+x-2=0得,x2+x-2≠0,故此选项错误;
B、把1代入x2+x=0得,x2+x≠0,故此选项错误;
C、∵△=32+4×4>0,∴方程x2+3x-4=0有两个不相等的实数根,故此选项正确;
D、∵△=-16<0,∴方程x2+4=0没有实数根,故此选项错误;
故选C.
点评 此题考查了一元二次方程的解,根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:填空题
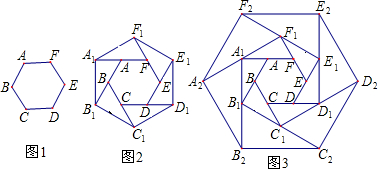
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
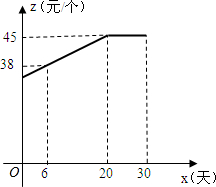 商人陈某打算对现有门面进行转型投资.经过考察,发现其门面所在的融侨公园附近有几所规模不小的学校却没有相应的文具店.为了保证投资利益,陈某决定针对某些常用文具进行调研.该门面在开学前采购了一种今年新上市的文具袋,准备9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后,得知日销量y(个)与销售时间x天之间有如下关系:y=-2x+80(1≤x≤30,且x为整数);又知销售价格z(元/个)与销售时间x之间的函数关系满足如图所示的函数图象.
商人陈某打算对现有门面进行转型投资.经过考察,发现其门面所在的融侨公园附近有几所规模不小的学校却没有相应的文具店.为了保证投资利益,陈某决定针对某些常用文具进行调研.该门面在开学前采购了一种今年新上市的文具袋,准备9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后,得知日销量y(个)与销售时间x天之间有如下关系:y=-2x+80(1≤x≤30,且x为整数);又知销售价格z(元/个)与销售时间x之间的函数关系满足如图所示的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2+b2=(a+b)2 | B. | xy+xz+x=x(y+z) | C. | x2+x3=x3 | D. | a2-2ab+b2=(a-b)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
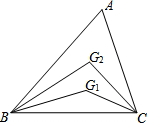 已知如图:△ABC中,∠ABC的三等分线与∠ACB的三等分线分别相交于G1,G2,
已知如图:△ABC中,∠ABC的三等分线与∠ACB的三等分线分别相交于G1,G2,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com