
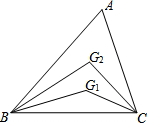
 已知如图:△ABC中,∠ABC的三等分线与∠ACB的三等分线分别相交于G1,G2,
已知如图:△ABC中,∠ABC的三等分线与∠ACB的三等分线分别相交于G1,G2,分析 (1)根据三角形的内角和定理可得∠ABC+∠ACB=138°,再由角的三等分线可得G2∠BC+∠G2CB,即可求得∠BG2C的度数;进一步在△BG1C中,得出∠G1BC+∠G1CB,求得∠BG1C;
(2)(3)由(1)得出结论直接猜想得出答案即可.
解答 解:(1)∵∠A=75°,
∴∠ABC+∠ACB=180°-75°=105°,
∴∠G2BC+∠G2CB=$\frac{2}{3}$(∠ABC+∠ACB)°=70°,
∴∠BG2C=180°-70°=110°.
∴∠G1BC+∠G1CB=$\frac{1}{3}$(∠ABC+∠ACB)=35°,
∴∠BG1C=180°-35°=145°.
(2)∠BG1C=180°-$\frac{1}{3}$(∠ABC+∠ACB)=180°-$\frac{1}{3}$(180°-∠A)=120°+$\frac{1}{3}$∠A;
∠BG2C=180°-$\frac{2}{3}$(∠ABC+∠ACB)=180°-$\frac{2}{3}$(180°-∠A)=60°+$\frac{2}{3}$∠A.
故答案为:145°,110°(2)$120°+\frac{1}{3}∠A$(3)$60°+\frac{2}{3}∠A$.
点评 本题考查的是三角形内角和定理,求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.


科目:初中数学 来源: 题型:选择题
| A. | 方程x2+x-2=0有一根为-1 | |
| B. | 方程x2+x=0有一根为1 | |
| C. | 方程x2+3x-4=0有两个不相等的实数根 | |
| D. | 方程x2+4=0有两个实数根,并且这两根互为相反数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表.五项素质考评得分表(单位:分):
学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表.五项素质考评得分表(单位:分):| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 甲班 | 10 | 10 | 6 | 10 | 7 |
| 乙班 | 10 | 8 | 8 | 9 | 8 |
| 丙班 | 9 | 10 | 9 | 6 | 9 |
| 班级 | 平均分 | 众数 | 中位数 |
| 甲班 | 8.6 | 10 | ③ |
| 乙班 | 8.6 | ② | 8 |
| 丙班 | ① | 9 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com